Produto vetorial

Dados um vetor: $\vec{u}=x_1\vec{i}+y_1\vec{j}+z_1\vec{k}$, e um outro vetor: $\vec{v}=x_2\vec{i}+y_2\vec{j}+z_2\vec{k}$, o produto vetorial $\vec{u}\times \vec{v}$, também representado como $\vec{u}\wedge \vec{v}$ é dado por:

$$\vec{u}\times \vec{v}=\left|\begin{array}{ccc}\vec{i}& \vec{j}& \vec{k}\\ x_1& y_1& z_1\\ x_2& y_2& z_2\end{array}\right|=\left|\begin{array}{cc}{y}_1& z_1\\ y_2& z_2\end{array}\right|\vec{i}-\left|\begin{array}{cc}{x}_1& z_1\\ x_2& z_2\end{array}\right|\vec{j}+\left|\begin{array}{cc}{x}_1& y_1\\ x_2& y_2\end{array}\right|\vec{k}$$

É importante destacar que o produto vetorial é um vetor, não um escalar (número real). Levando em conta as propriedades dos determinantes, é possível tirar algumas conclusões sobre produtos vetoriais:

1. No caso do produto vetorial a ordem dos fatores importa, isso se dá pela troca de ordem dos elementos no cálculo de determinantes inverter o sinal dos determinantes intermediários de ordem 2, implicando em: $\vec{v}\times \vec{u}=-(\vec{u}\times \vec{v})$, ou seja, $\vec{v}\times \vec{u}\ne \vec{u}\times \vec{v}$.
2. O produto vetorial $\vec{u}\times \vec{v}$ é igual a $0$ se e somente se $\vec{u}//\vec{v}$, pois assim todos os determinantes intermediários de ordem 2 teriam suas linhas proporcionais. Analogamente $\vec{u}\times \vec{0}=0$, pois todos os determinanates intermediários teríam uma linha de zeros.

Características

Direção

O vetor $\vec{u}\times \vec{v}$ é simultaneamente ortogonal a $\vec{u}$ e $\vec{v}$. Portanto $(\vec{u}\times \vec{v})\vec{u}=0$ e $(\vec{u}\times \vec{v})\vec{v}=0$

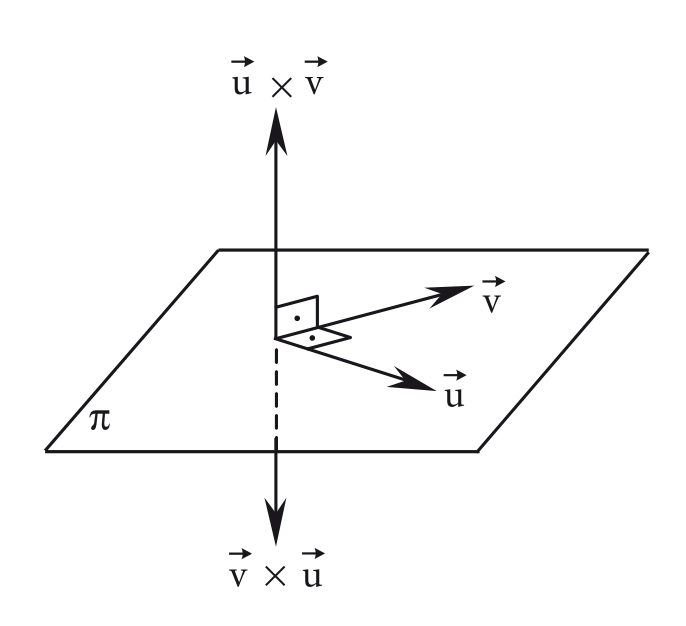
Sentido

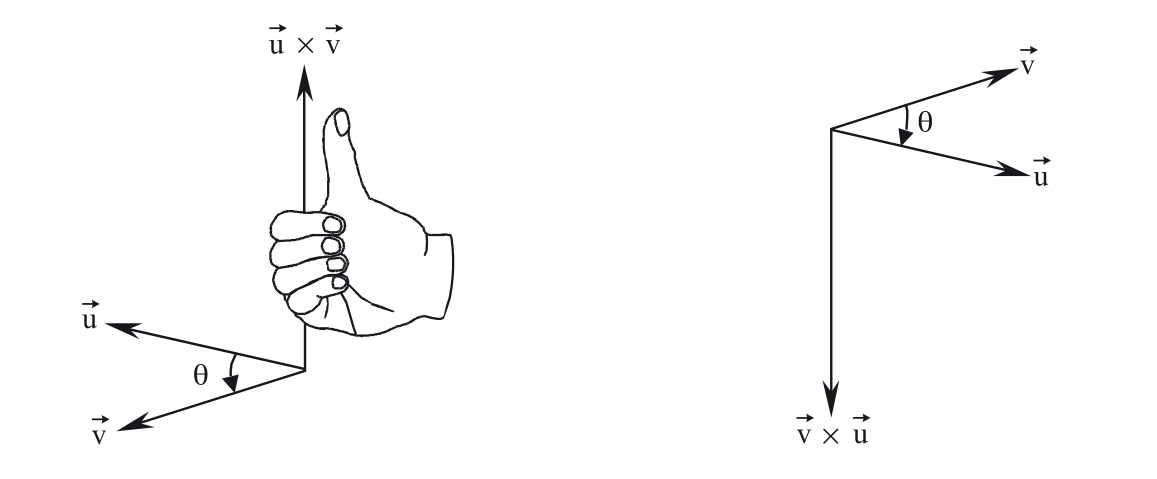
O sentido do produto vetorial pode ser intuitivamente determinado através da regra da mão direita ilustrada na figura, a ideia é fazer com que os dedos da mão direita apontem no sentido da rotação do ângulo que vai do primeiro até o segundo vetor, então o polegar indica o sentido correto do vetor resultante.

Módulo

A seguinte definição do módulo de um produto vetorial é obtida a partir da identidade de Lagrange.
Sendo $\theta$ o ângulo entre os vetores $\vec{u}$ e $\vec{v}$, então

$$|\vec{u}\times \vec{v}|=|\vec{u}||\vec{v}|\sin \theta$$

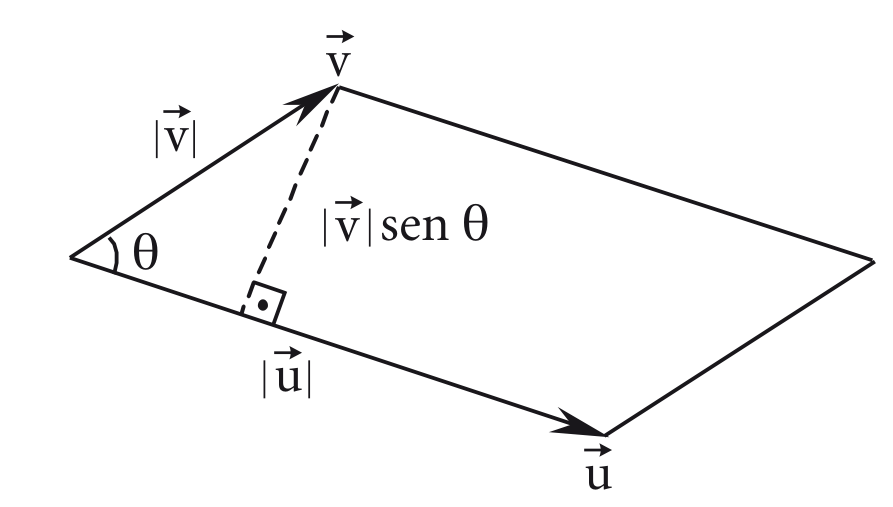
A área de um paralelogramo determinado pelos vetores $\vec{u}$ e $\vec{v}$ é numericamente igual ao módulo do vetor $\vec{u}\times \vec{v}$, ou seja:

$$A=|\vec{u}\times \vec{v}|$$

E também, a altura desse paralelogramo é definida por:

$$h=|\vec{v}|\sin \theta$$