O plano

Seja $A(x_1,y_1,z_1)$ um ponto pertencente ao plano $\pi$ e $\vec{n}=(a,b,c)$, $\vec{n}\ne \vec{0}$, um vetor ortogonal (normal) ao plano $pi$.

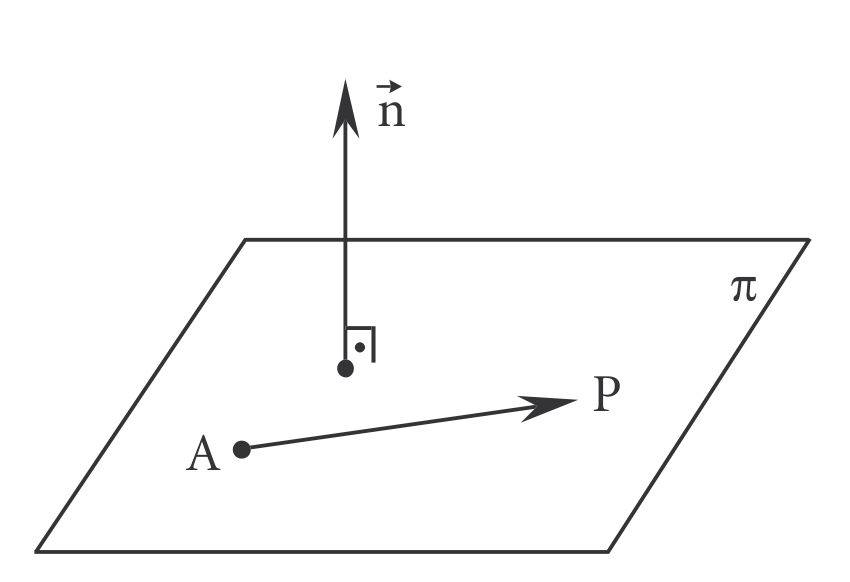
Como $\vec{n}\perp \pi$, $\vec{n}$ é ortogonal a todo vetor representado em $\pi$, então um ponto $P(x,y,z)$ percente a $\pi$ se, e somente se, o vetor $\overrightarrow{AP}$ é ortogonal a $\vec{n}$. A partir disso obtem-se a equação geral do plano:

$$ax+by+cz+d=0$$

sendo que:

$$d=-a{x}_1-b{y}_1-c{z}_1$$

Um caso específico é quando um plano $\pi$ intercepta os eixos coordenados nos pontos $(p,0,0)$, $(0,q,0)$ e $(0,0,r)$, com $p\cdot q\cdot r\ne 0$. Se isso ocorre, então $\pi$ admite também a equaçào segmentária do plano:

$$\frac{x}{p}+\frac{y}{q}+\frac{z}{r}=1$$

Essa equação é equivalente à equação geral para esses planos, porém pode ser mais conveniente encontrá-la em determinados contextos.

Uma outra forma de obter a equação geral de um plano é através do produto misto. Seja $A(x_0,y_0,z_0)$ um ponto pertencente a um plano $\pi$ e $\vec{u}=(a_1,b_1,c_1)$ e $\vec{u}=(a_1,b_1,c_1)$ dois vetores paralelos a $\pi$, e não paralelos entre si. Sendo $P(x,y,z)$ um ponto qualquer do plano $\pi$, $\overrightarrow{AP}$, $\vec{u}$ e $\vec{v}$ são coplanares, portanto o produto misto deles é nulo, ou seja:

$$(\overrightarrow{AP},\vec{u},\vec{v})=0$$

Assim, podemos obter uma equação geral do plano mantendo as incógnitas do ponto $P$ e desenvolvendo o produto misto.

Equação vetorial e equações paramétricas do plano

Seja $A(x_0,y_0,z_0)$ um ponto pertencente a um plano $\pi$ e $\vec{u}=(a_1,b_1,c_1)$ e $\vec{u}=(a_1,b_1,c_1)$ dois vetores paralelos a $\pi$, e não paralelos entre si.

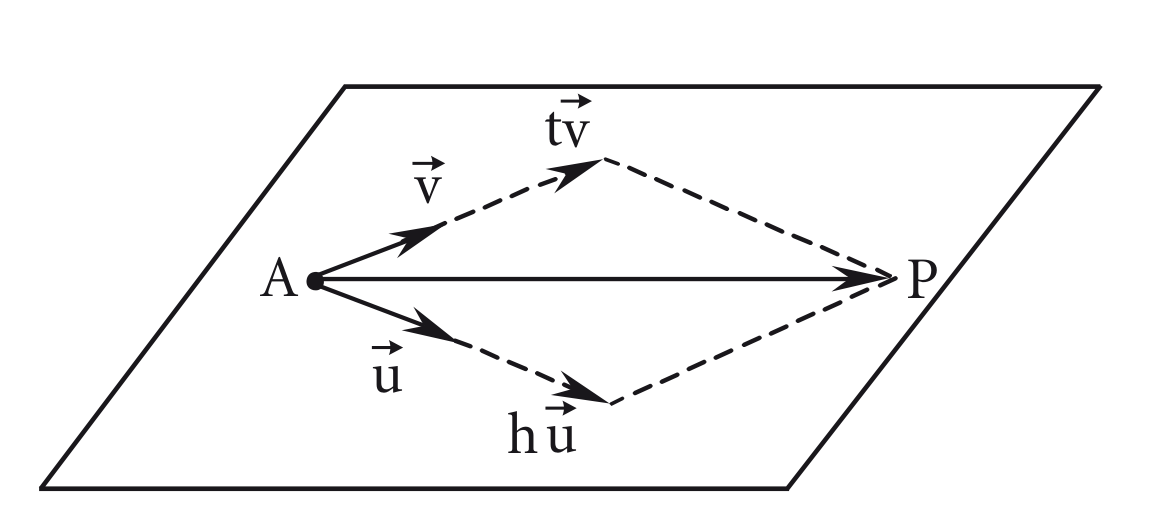
Para todo ponto $P$ do plano, os vetores $\overrightarrow{AP}$, $\vec{u}$ e $\vec{v}$ são coplanares, chamamos os vetores $\vec{u}$ e $\vec{v}$ de vetores diretores de $\pi$. A partir disso obtem-se a equação vetorial do plano:

$$(x,y,z)=(x_0,y_0,z_0)+h(a_1,b_1,c_1)+t(a_2,b_2,c_2),h,t\in \mathbb{R}$$

Pela condição de igualdade, podemos definir as equações paramétricas de $\pi$ com parâmetros $h$ e $t$:

$$\{\begin{array}{l}x=x_0+a_{1}h+a_{2}t\\ y=y_0+b_{1}h+b_{2}t\\ z=z_0+c_{1}h+c_{2}t\end{array}h,t\in \mathbb{R}$$

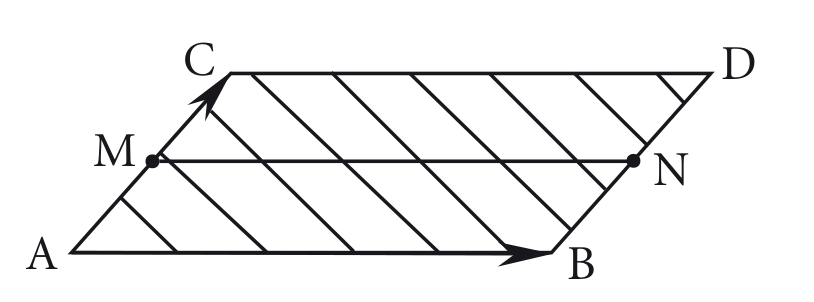
Equação vetorial de um paralelogramo

Dados os pontos não colineares $A$, $B$ e $C$, os vetores $\overrightarrow{AB}$ e $\overrightarrow{AC}$ determinam o paralelogramo cuja equação vetorial é

$$P=A+h(\overrightarrow{AB})+t(\overrightarrow{AC})h,t\in [0,1]$$

Casos particulares da equação geral do plano

Caso um ou mais coeficientes da equação geral do plano $ax+by+cz+d=0$ seja nulo, o plano ocupará uma posição particular em relação aos eixos ou planos coordenados.

1. Se $d=0$, então o plano passa pela origem.
2. Se o coeficiente de apenas uma coordenada for nulo, então o plano é paralelo ao eixo dessa coordenada, ou seja, o plano é paralelo ao eixo da variável ausente na equação.
3. Se dois coeficientes duas coordenadas forem nulos, então o plano é paralelo ao plano formado pelos eixos dessas coordenadas. Por exemplo: $\pi :z=k\therefore \pi //xOy$

Ângulo de dois planos

Sejam os planos ${\pi }_1$ e ${\pi }_2$ com vetores normais ${\vec{n}}_1$ e $\overrightarrow{n_2}$, respectivamente:

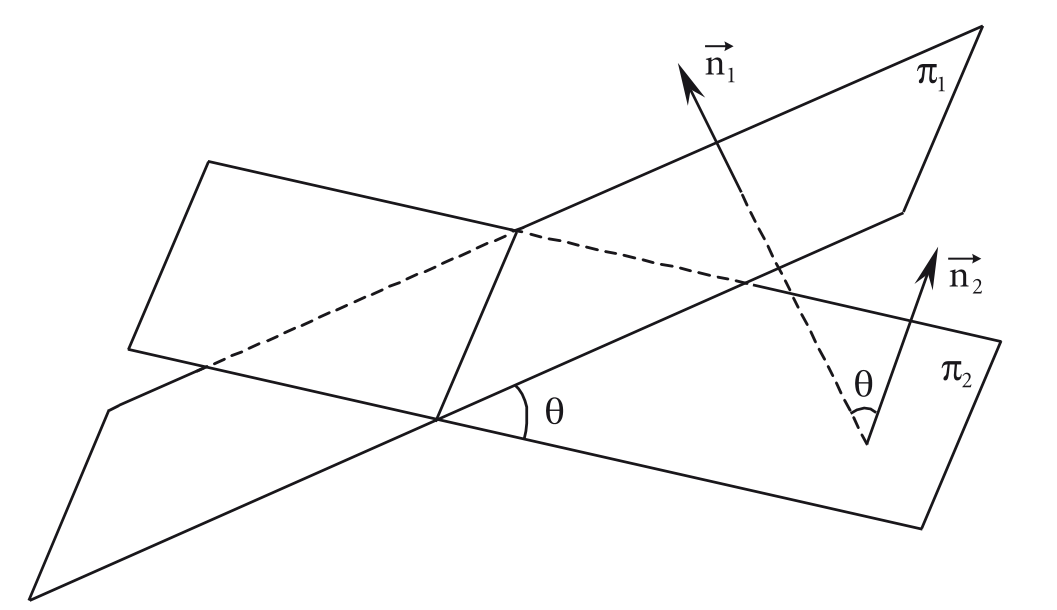
O ângulo de dois planos ${\pi }_1$ e ${\pi }_2$ é o menor ângulo que um vetor normal a ${\pi }_1$ forma com um vetor normal a ${\pi }_2$. Sendo $\theta$ esse ângulo, tem-se:

$$\cos \theta =\frac{|\overrightarrow{n_1}\cdot \overrightarrow{n_2}|}{|\overrightarrow{n_1}||\overrightarrow{n_2}|}0\le \theta \le \frac{\pi }{2}$$

Planos perpendiculares

Sejam os planos ${\pi }_1$ e ${\pi }_2$ com vetores normais ${\vec{n}}_1$ e $\overrightarrow{n_2}$, respectivamente.

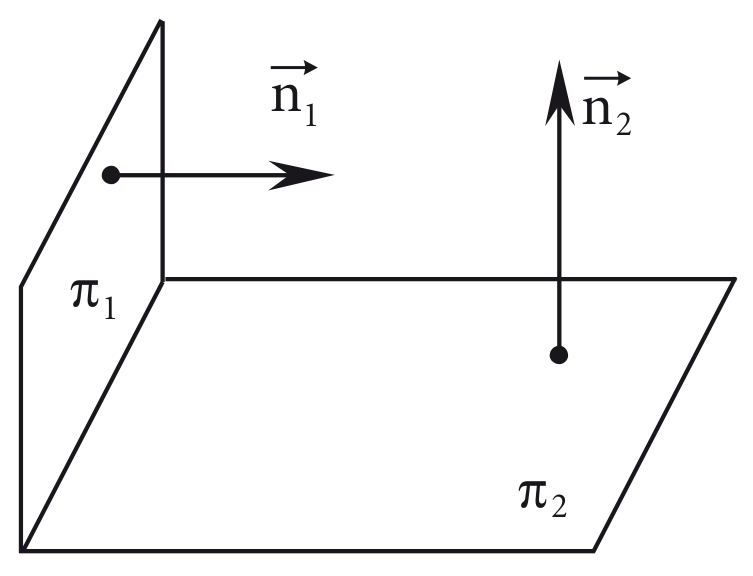
Então, a perpendicularidade dos planos depende diretamente da perpendicularidade entre seus vetores normais.

$${\pi }_1\perp {\pi }_2\iff \overrightarrow{n_1}\perp \overrightarrow{n_2}\iff \overrightarrow{n_1}\cdot \overrightarrow{n_2}=0$$

Paralelismo e perpendicularismo entre reta e plano

Seja $r$ uma reta com vetor diretor $\vec{v}$ e um plano $\pi$, sendo $\vec{n}$ um vetor normal a $\pi$.

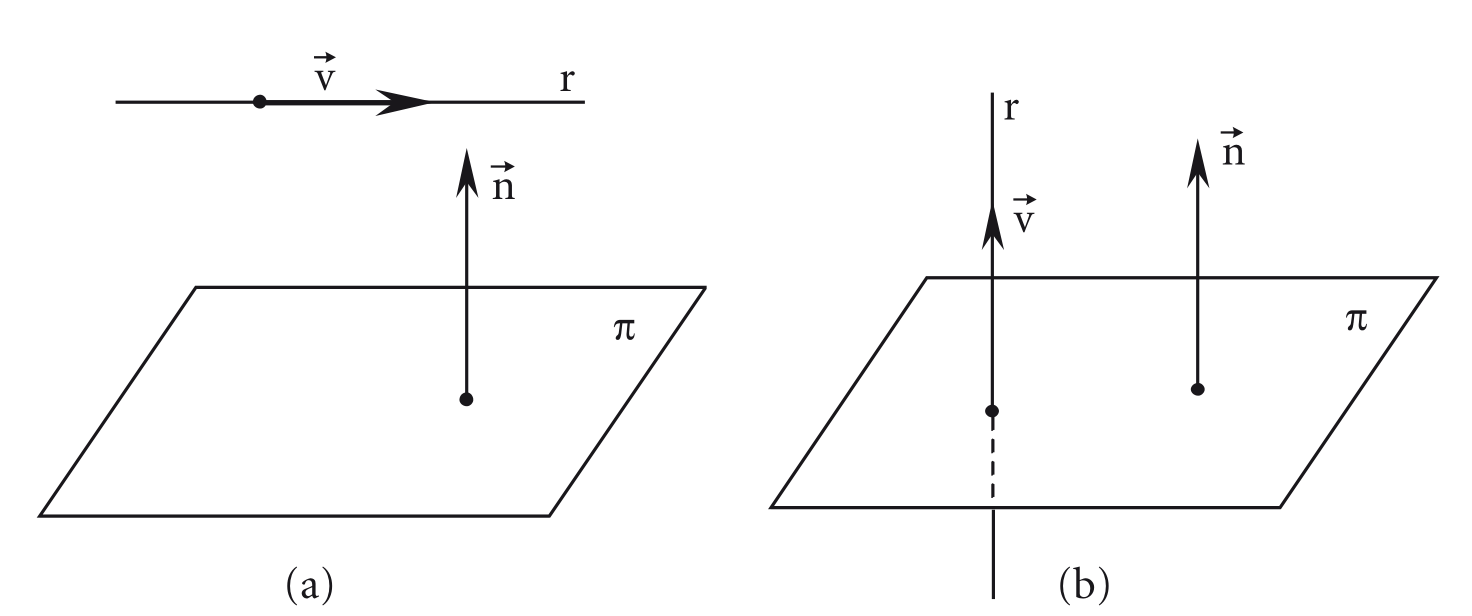
Então, o paralelismo e a perpendicularidade entre um plano e uma reta depende diretamente do paralelismo e da perpendicularidade entre o vetor diretor da reta e o vetor normal ao plano.

$$r//\pi \iff \vec{v}\perp \vec{n}\iff \vec{v}\cdot \vec{n}=0$$ $$r\perp \pi \iff \vec{v}//\vec{n}\iff \vec{v}=\alpha \vec{n}$$

Reta contida em um plano

Uma reta $r$ está contida no plano $\pi$ se qualquer uma das duas condições forem verdadeiras:

1. Dois pontos $A$ e $B$ de $r$ forem também de $\pi$
2. $\vec{v}\cdot \vec{n}=0$, em que $\vec{v}$ é um vetor diretor de $r$ e $\vec{n}$ um vetor normal a $\pi$ e $A\in \pi$, sendo $A\in r$.

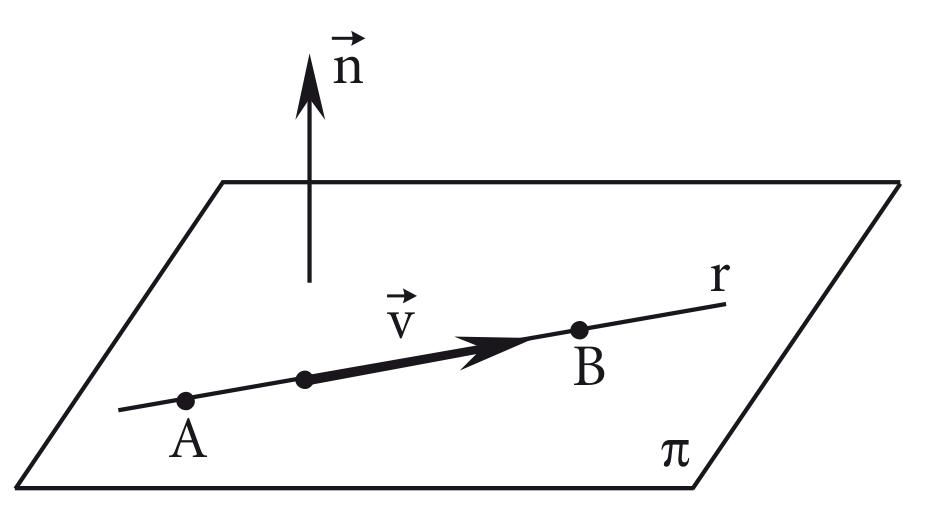
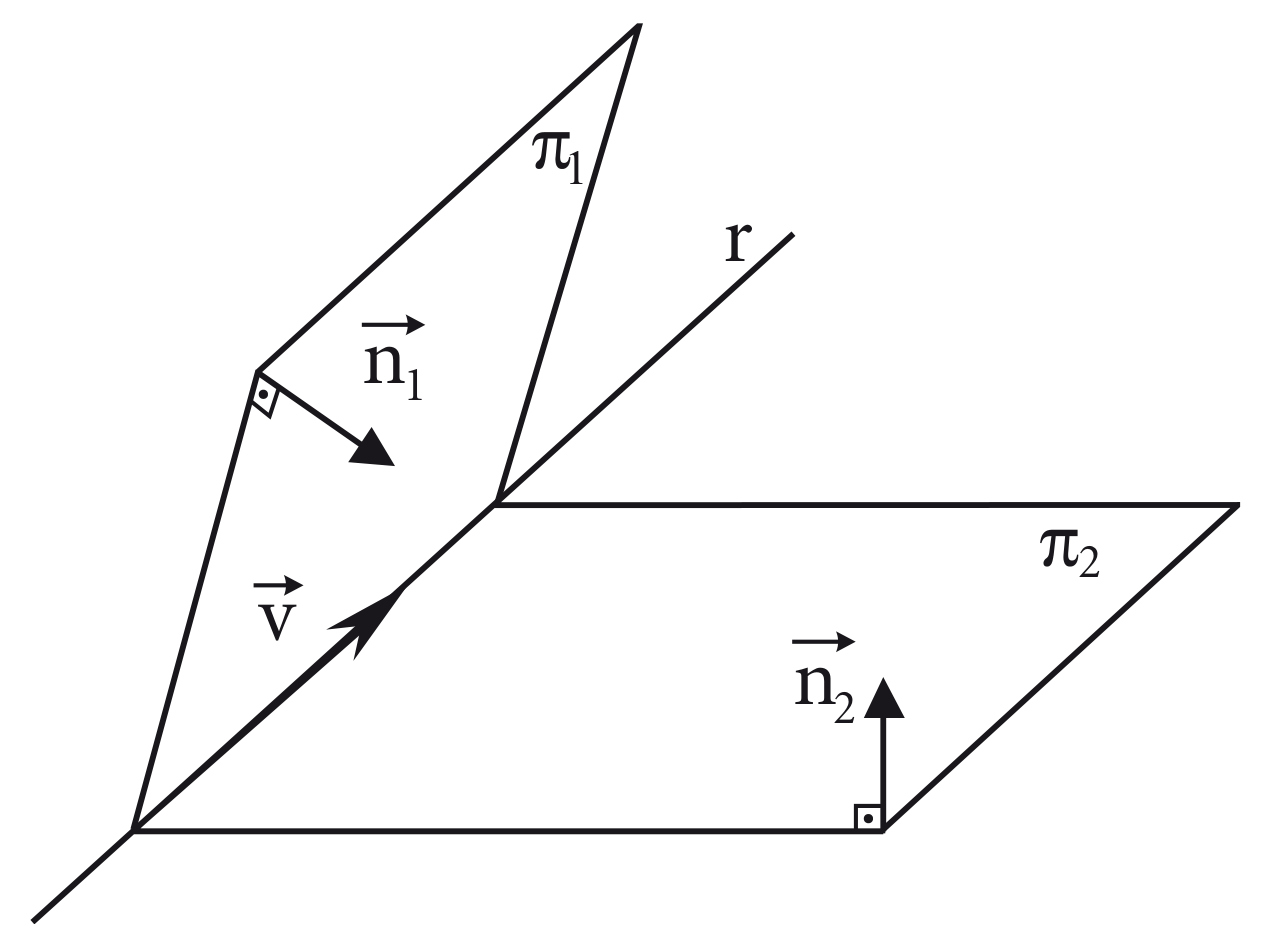
Intersecção de dois planos

A interseção entre dois planos é definida por uma reta $r$ que contém os pontos em comum entre os dois planos. Existem dois procedimentos para encontrar a intersecção entre dois planos:

1. Como $r$ está contida nos dois planos, as coodernadas de qualquer ponto $(x,y,z)\in r$ devem satisfazer, simultâneamente, as equações de ambos os planos. Sendo assim podemos definir $r$ como um sistema de duas equações: as equações dos planos.
2. Podemos definir um ponto $A$ que esteja contido em ambos os planos e um vetor $\vec{v}$ que seja simultaneamente ortogonal aos vetores normais dos dois planos, ou seja, $\vec{v}$ é definido pelo produto vetorial entre os vetores normais dos dois planos. A partir disso podemos definir a reta através de um ponto e um vetor.

Ângulo entre reta e plano

Dada uma reta $r$ com vetor diretor $\vec{v}$ e um plano $\pi$ com vetor normal $\vec{n}$, o ângulo $\theta$ entre $r$ e $\pi$ é dado por:

$$\sin \theta =\frac{|\vec{v}\cdot \vec{n}|}{|\vec{v}||\vec{n}|}0\le \theta \le \frac{\pi }{2}$$

Intersecção de reta com plano

Para determinar a intersecção de uma reta $r$ com um plano $\pi$ basta encontrar um ponto $A$ tal que $A\in r$ e $A\in \pi$ simultaneamente. Isso pode ser feito substituindo cada uma das variáveis da equação geral do plano pela uma equação paramétrica da reta correspondente àquela coordenada. Dessa forma é possível encontrar um parâmetro $t$ que indica qual ponto da reta $r$ pertence também ao plano $\pi$.