Produto misto

Dados três vetores: $\vec{u}=x_1\vec{i}+y_1\vec{j}+z_1\vec{k}$, $\vec{v}=x_2\vec{i}+y_2\vec{j}+z_2\vec{k}$ e $\vec{w}=x_3\vec{i}+y_3\vec{j}+z_3\vec{k}$, tomados nessa ordem, o produto misto é o número real $\vec{u}\cdot (\vec{v}\times \vec{w})$, também indicado por $(\vec{u},\vec{v},\vec{w})$, é dado por:

$$\vec{u}\cdot (\vec{v}\times \vec{w})=\left|\begin{array}{ccc}{x}_1& y_1& z_1\\ x_2& y_2& z_2\\ x_3& y_3& z_3\end{array}\right|$$

As seguintes propriedades do produto misto decorrem principalmente das propriedades dos determinantes.

1. O produto misto $(\vec{u},\vec{v},\vec{w})$ muda de sinal ao trocarmos a posição de dois vetores.
2. $(\vec{u}+\vec{x},\vec{v},\vec{w})=(\vec{u},\vec{v},\vec{w})+(\vec{x},\vec{v},\vec{w})$
3. $(\alpha \vec{u},\vec{v},\vec{w})=(\vec{u},\alpha \vec{v},\vec{w})=(\vec{u},\vec{v},\alpha \vec{w})=\alpha (\vec{u},\vec{v},\vec{w})$
4. $(\vec{u},\vec{v},\vec{w})=0$ se, e somente se, os três vetores forem coplanares.

Interpretação geométrica

Geometricamente, o produto misto $\vec{u}\cdot (\vec{v},\vec{w})$ é igual, em módulo, ao volume do paralelepípedo de arestas determinadas pelos vetores não coplanares $\vec{u}$, $\vec{v}$ e $\vec{w}$.

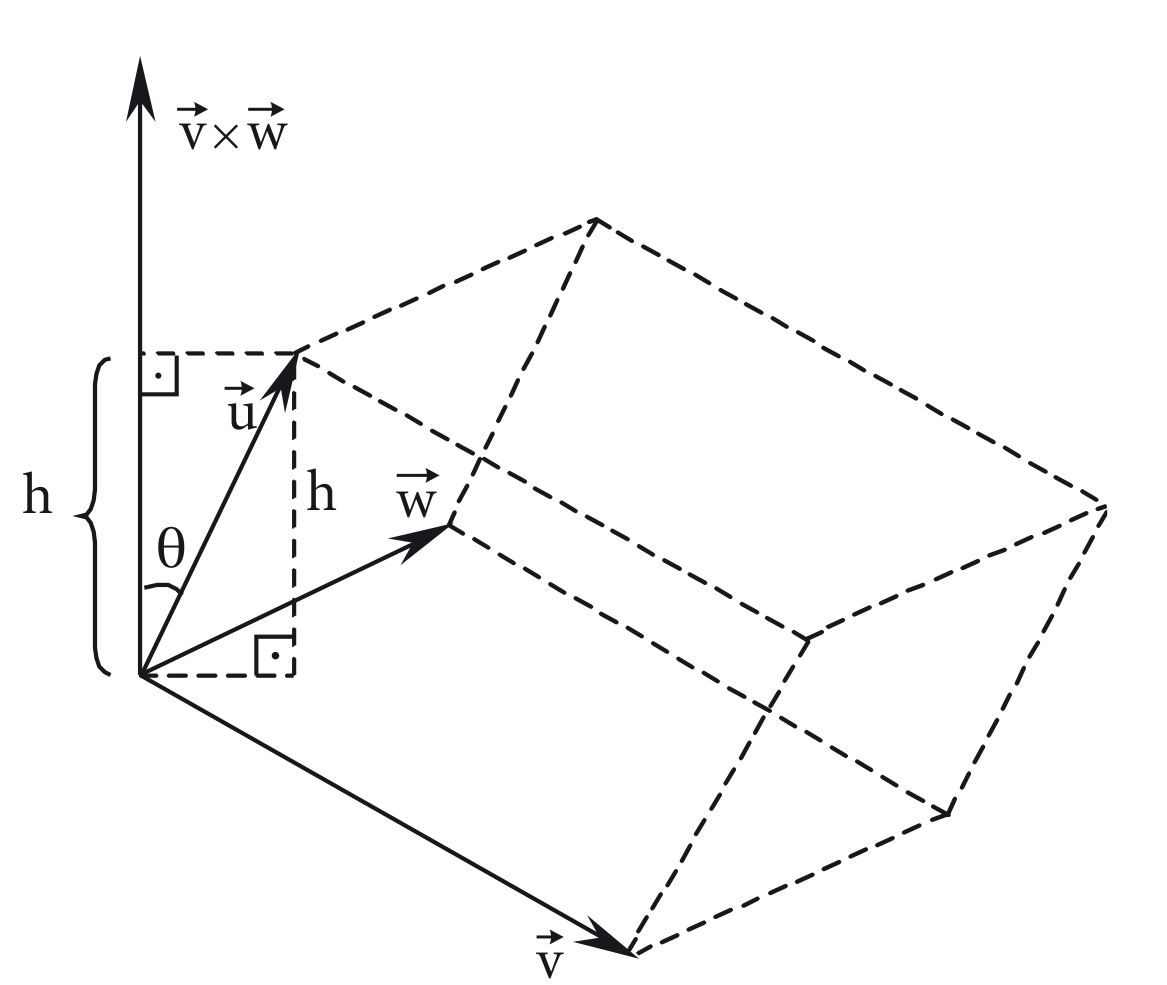
A área da base do paralelepípedo é dada por $|\vec{v}\times \vec{w}|$, como definido nos produtos vetoriais. Sendo $\theta$ o ângulo entre $\vec{u}$ e $|\vec{v}\times \vec{w}|$, a altura do paralelepípedo é dada por:

$$h=|\vec{u}||\cos \theta |$$

Sendo assim, o volume $V$ do paralelepípedo é dado por:

$$V=|\vec{v}\times \vec{w}||\vec{u}||\cos \theta |$$

ou seja,

$$V=|(\vec{u},\vec{v},\vec{w})|$$

Volume do tetraedro

Considerando $A$, $B$, $C$ e $D$ pontos não coplanares, em que $\overrightarrow{AB}$, $\overrightarrow{AC}$ e $\overrightarrow{AD}$ determinam um paralelepípedo de volume definido por:

$$V=|(\overrightarrow{AB},\overrightarrow{AC},\overrightarrow{AD})|$$

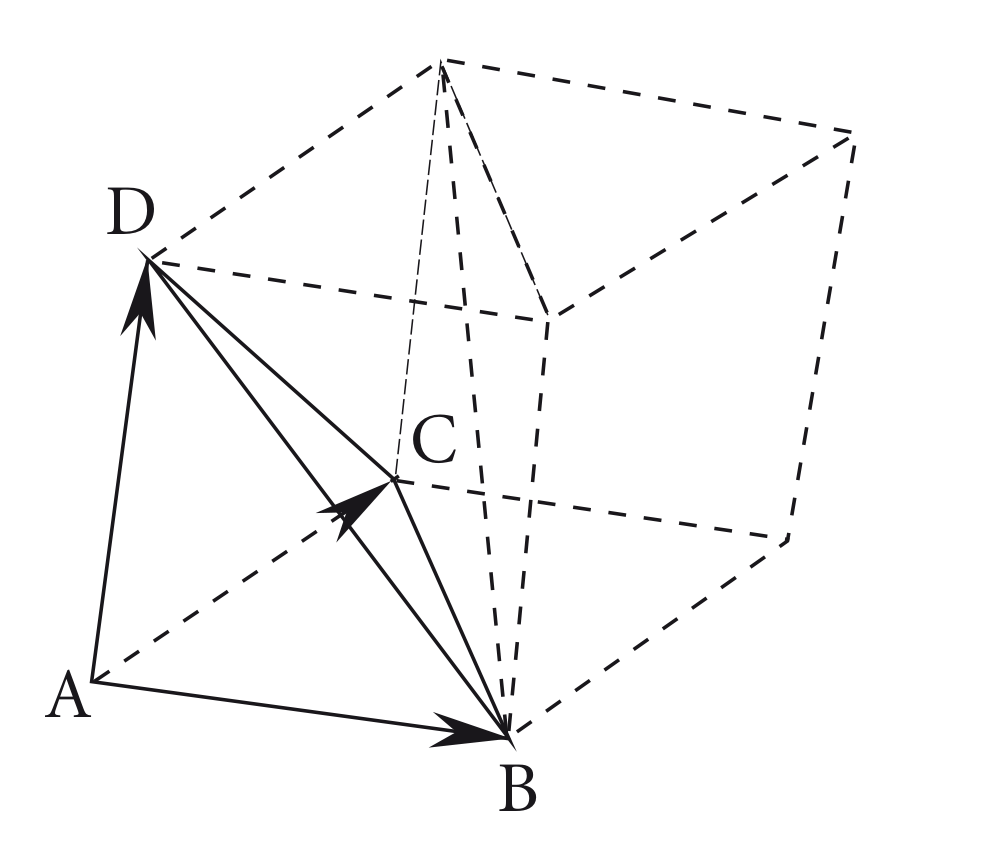
Podemos repartir o paralelepípedo em dois prismas triangulares de mesmo tamanho, com seus volumes $V_p$ definidos por:

$$V_p=\frac{1}{2}V$$

Podemos ainda repartir cada prisma em três pirâmides de mesmo volume, sendo uma delas o tetraedro $ABCD$, de volume $V_t$ dado por:

$$V_t=\frac{1}{3}{V}_p=\frac{1}{6}V$$

ou seja,

$$V_t=\frac{1}{6}|(\overrightarrow{AB},\overrightarrow{AC},\overrightarrow{AD})|$$