Distância entre pontos
Dados os pontos e , a distância entre eles é , ou seja:
Distância de um ponto a uma reta
Dado um ponto no espaço e uma reta , para encontrar a distância do ponto à reta podemos usar a altura do paralelogramo:
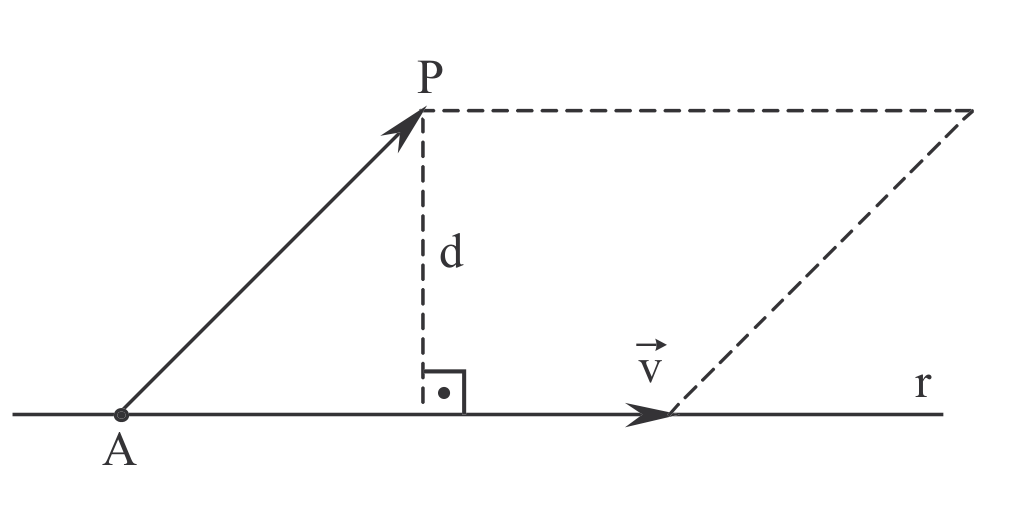
Tomando o vetor diretor da reta temos que:
Distância de ponto a plano
Dado um ponto e um plano , para calcular a distância tomamos um ponto qualquer e um vetor normal a .
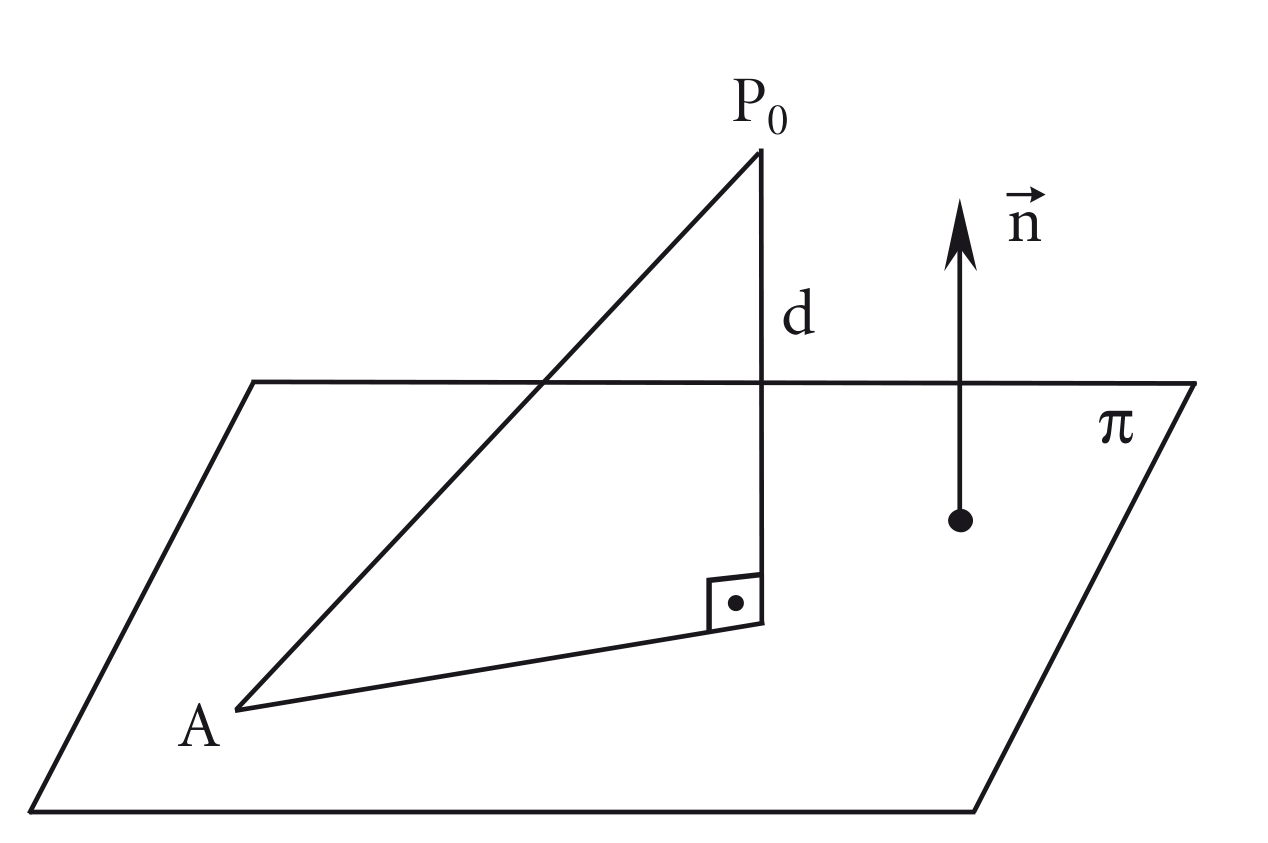
Podemos perceber que a distância é o módulo da projeção de na direção de , sendo assim, a partir da definição de projeção ortogonal define-se a seguinte expressão:
Distância entre duas retas
Dadas as retas e , o cálculo da distância depende da relação que elas estabelecem entre si:
- Se e são concorrentes, então , pois elas possuem um ponto em comum.
- Se e são paralelas, então , com , ou , com . Isso se dá pelo fato de que, se as retas são paralelas então a distância das retas é igual à distância de qualquer ponto em qualquer uma das retas à outra reta.
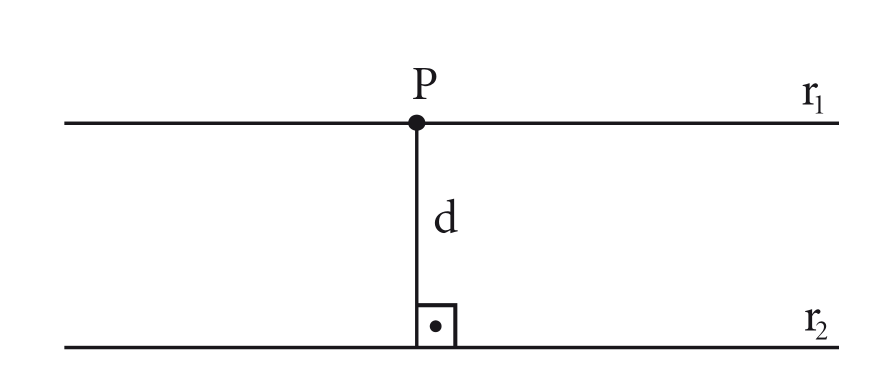
- Se e são reversas, então:
Sejam e as retas definidas pelos pontos e e pelos vetores diretores e , respectivamente. Os vetores , e determinam o paralelepípedo da figura cuja altura é a distância
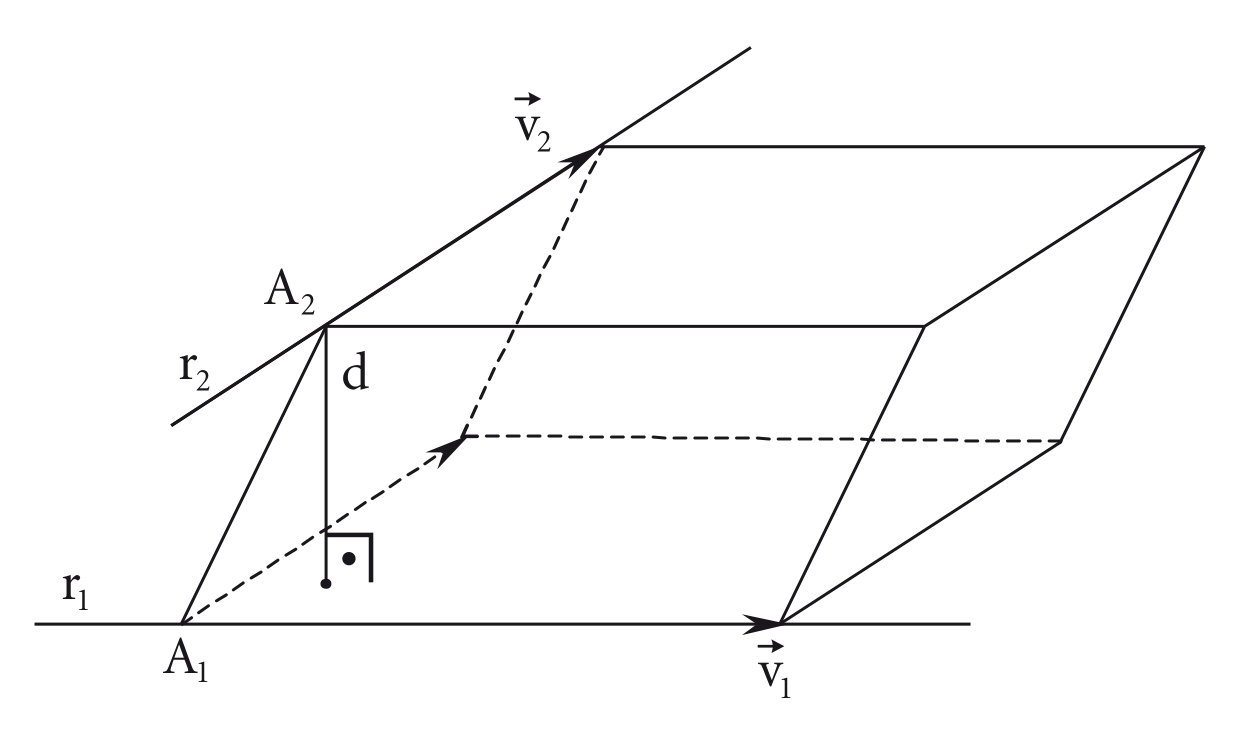
Usando a definição de volume chega-se na seguinte definição: