Produto escalar de vetores

Dados dois vetores $\vec{u}=x_1\vec{i}+y_1\vec{j}+z_1\vec{k}$ e $\vec{v}=x_2\vec{i}+y_2\vec{j}+z_2\vec{k}$, o produto escalar $\vec{u}\cdot \vec{v}$ é dado por:
$\vec{u}\cdot \vec{v}=x_1{x}_2+y_1{y}_2+z_1{z}_2$

Note que o produto escalar de dois vetores é um número real, não um vetor.
Algumas propriedades interessantes dos produtos escalares são as seguintes:

$$\begin{array}{rl}\vec{u}\cdot \vec{u}& =|\vec{u}{|}^2\\ |\vec{u}+\vec{v}{|}^2& =|\vec{u}{|}^2+2\vec{u}\cdot \vec{v}+|\vec{v}{|}^2\\ |\vec{u}-\vec{v}{|}^2& =|\vec{u}{|}^2-2\vec{u}\cdot \vec{v}+|\vec{v}{|}^2\\ (\vec{u}+\vec{v})\cdot (\vec{u}-\vec{v})& =|\vec{u}{|}^2-|\vec{v}{|}^2\end{array}$$

Definição geométrica

Usando a lei dos cossenos e as definições anteriores, é possível chegar na seguinte definição:

$$\vec{u}\cdot \vec{v}=|\vec{u}||\vec{v}|\cos \theta ,0^{\circ }\le \theta \le 180^{\circ }$$

Sendo $\theta$ o ângulo entre os vetores $\vec{u}$ e $\vec{v}$.
De maneira análoga à definição algébrica, temos as seguintes propriedades:

$$\begin{array}{rl}|\vec{u}+\vec{v}{|}^2& =|\vec{u}{|}^2+|\vec{v}{|}^2+2|\vec{u}||\vec{v}|\cos \theta \\ |\vec{u}-\vec{v}{|}^2& =|\vec{u}{|}^2+|\vec{v}{|}^2-2|\vec{u}||\vec{v}|\cos \theta \end{array}$$

Note que essa definição não depende das coordenadas dos vetores, apenas de seu módulo.
A partir disso é possível inferir uma condição para que dois vetores sejam orgotonais:
Dois vetores $\vec{u}$ e $\vec{v}$ são ortogonais se, e somente se, $\vec{u}\cdot \vec{v}=0$

Cálculo do ângulo de dois vetores

Dados os vetores $\vec{u}$ e $\vec{v}$, o ângulo $\theta$ formado por esses dois vetores é dado por:
$\cos \theta =\frac{\vec{u}\cdot \vec{v}}{|\vec{u}|\cdot |\vec{v}|}$

Ângulos diretores e cossenos diretores

Seja o vetor $\vec{v}=x\vec{i}+y\vec{j}+z\vec{k}$, os ângulos diretores de $\vec{v}$ são os ângulos $\alpha$, $\beta$, $\gamma$ que $\vec{v}$ forma com os vetores $\vec{i}$, $\vec{j}$ e $\vec{k}$ respectivamente. Da mesma forma, os cossenos diretores de $\vec{v}$ são os cossenos desses ângulos diretores, ou seja, $\cos \alpha$, $\cos \beta$ e $\cos \gamma$.

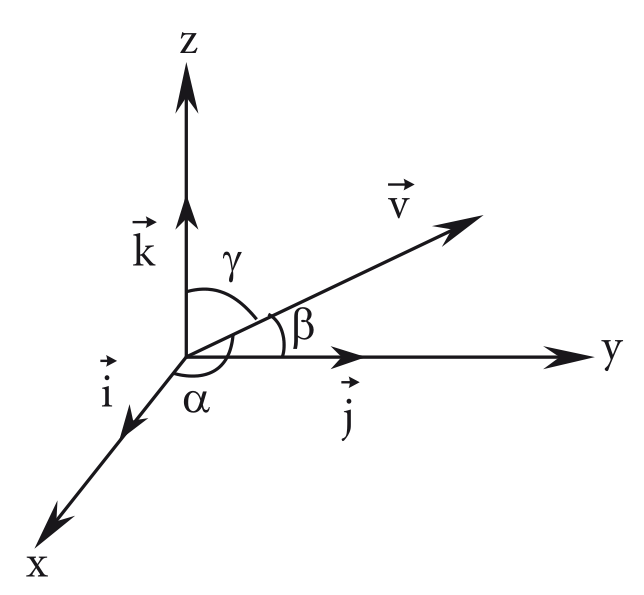
Utilizando as definições anteriores, é possível verificar que os valores dos cossenos diretores de $\vec{v}$ são precisamente os componentes do versor de $\vec{v}$, ou seja:

$$\begin{array}{rl}\cos \alpha & =\frac{x}{|\vec{v}|}\\ \cos \beta & =\frac{y}{|\vec{v}|}\\ \cos \gamma & =\frac{z}{|\vec{v}|}\end{array}$$

Isso implica que:

$${\cos }^2\alpha +{\cos }^2\beta +{\cos }^2\gamma =1$$

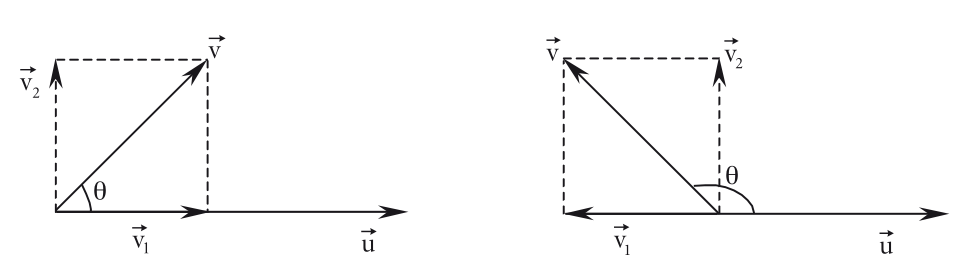
Projeção de um vetor sobre outro

Sejam os vetores $\vec{u}$ e $\vec{v}$, e $\theta$ o ângulo entre eles, se decompormos um dos vetores, por exemplo $\vec{v}=\overrightarrow{v_1}+\overrightarrow{v_2}$, sendo $\overrightarrow{v_1}//\vec{u}$ e $\overrightarrow{v_2}\perp \vec{u}$. Quando isso ocorre o vetor $\overrightarrow{v_1}$ é chamado de projeção ortogonal de $\vec{v}$ sobre $\vec{u}$, e indicado por:

$$\begin{array}{r}\overrightarrow{v_1}={\text{proj}}_{\vec{u}}\vec{v}=\left(\frac{\vec{v}\cdot \vec{u}}{|\vec{u}{|}^2}\right)\vec{u}\end{array}$$