Uma rede neural é um algoritmo de Aprendizado supervisionado que consiste em uma rede composta por diversos nós chamados neurônios conectados através das diversas camadas da rede. O objetivo das redes neurais é reconhecer padrões entre as variáveis de entrada através de um processo que simula o funcionamento do cérebro humano.
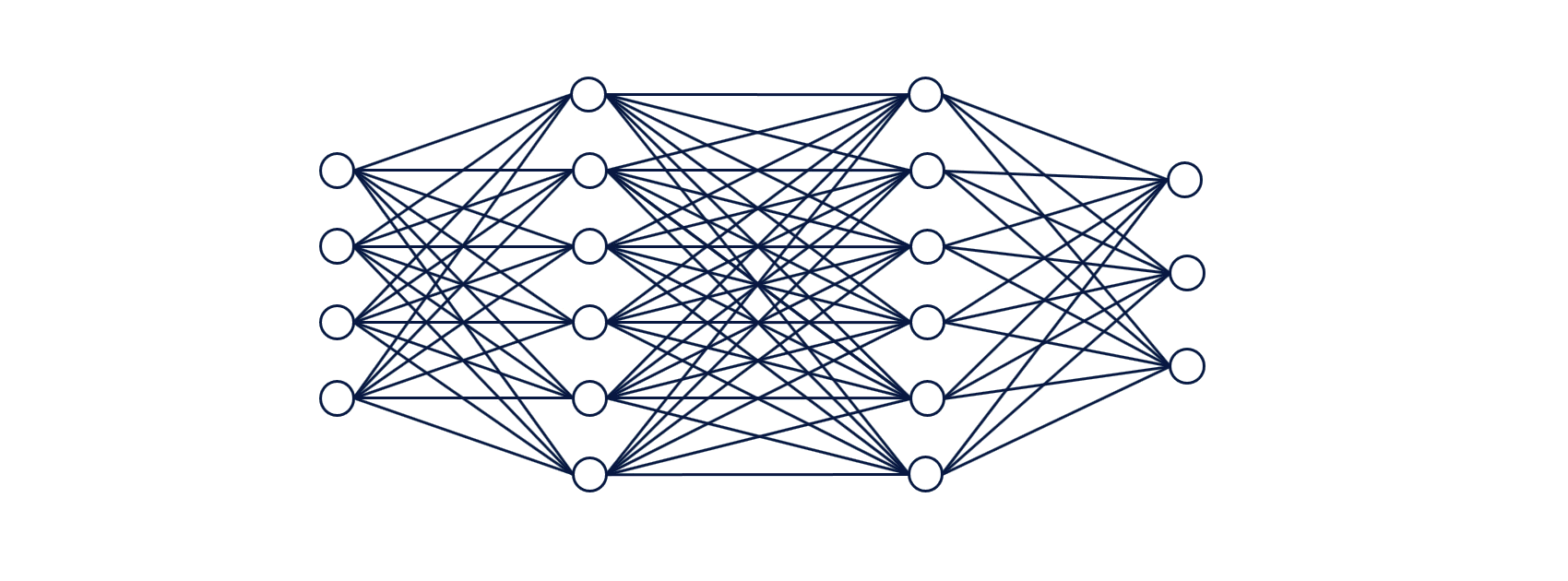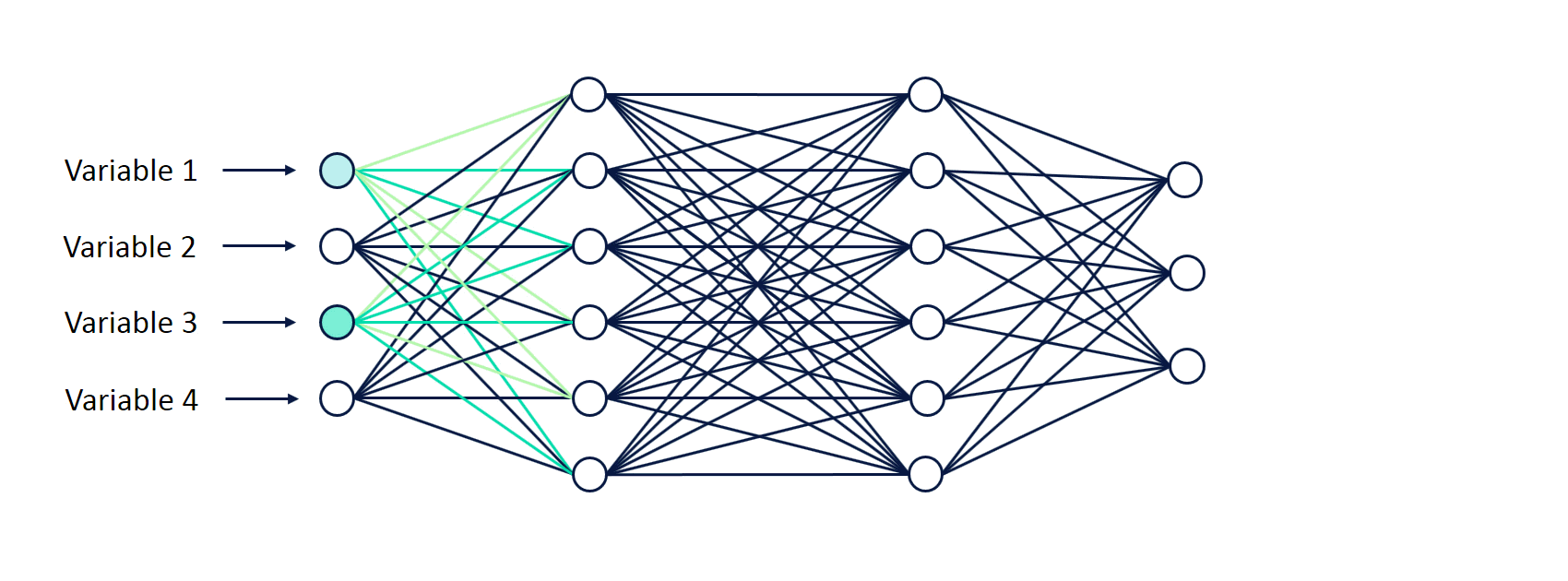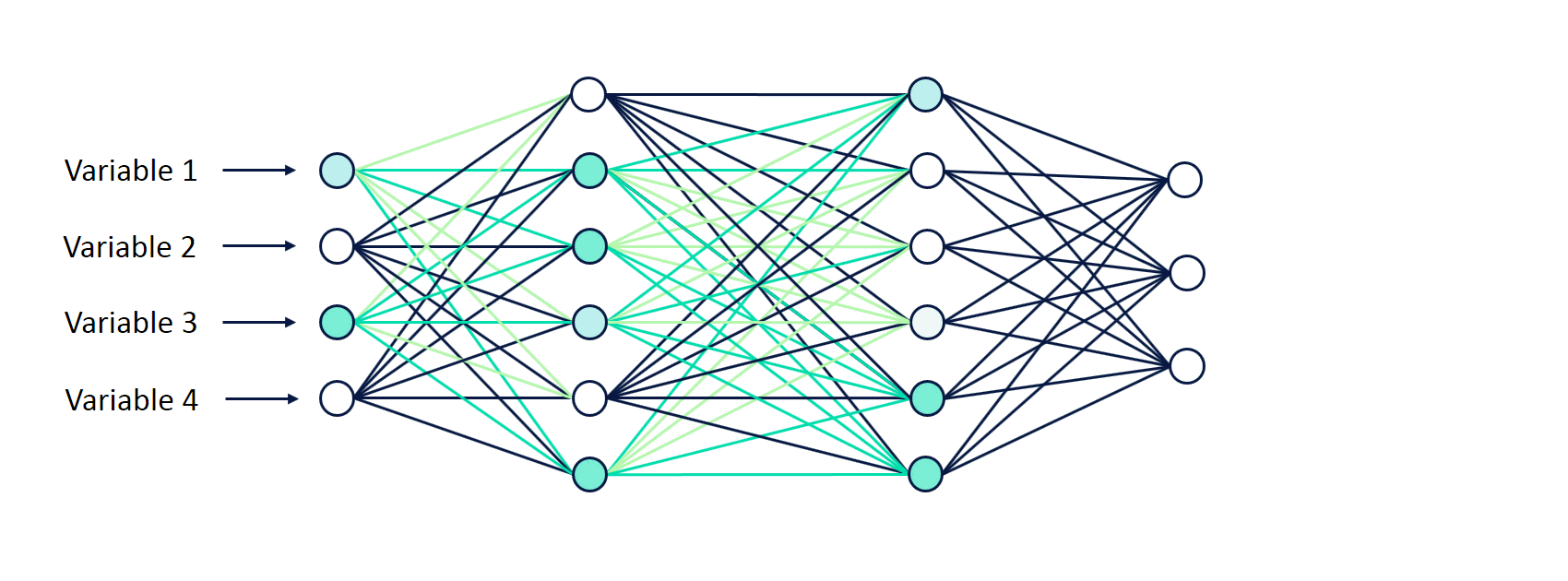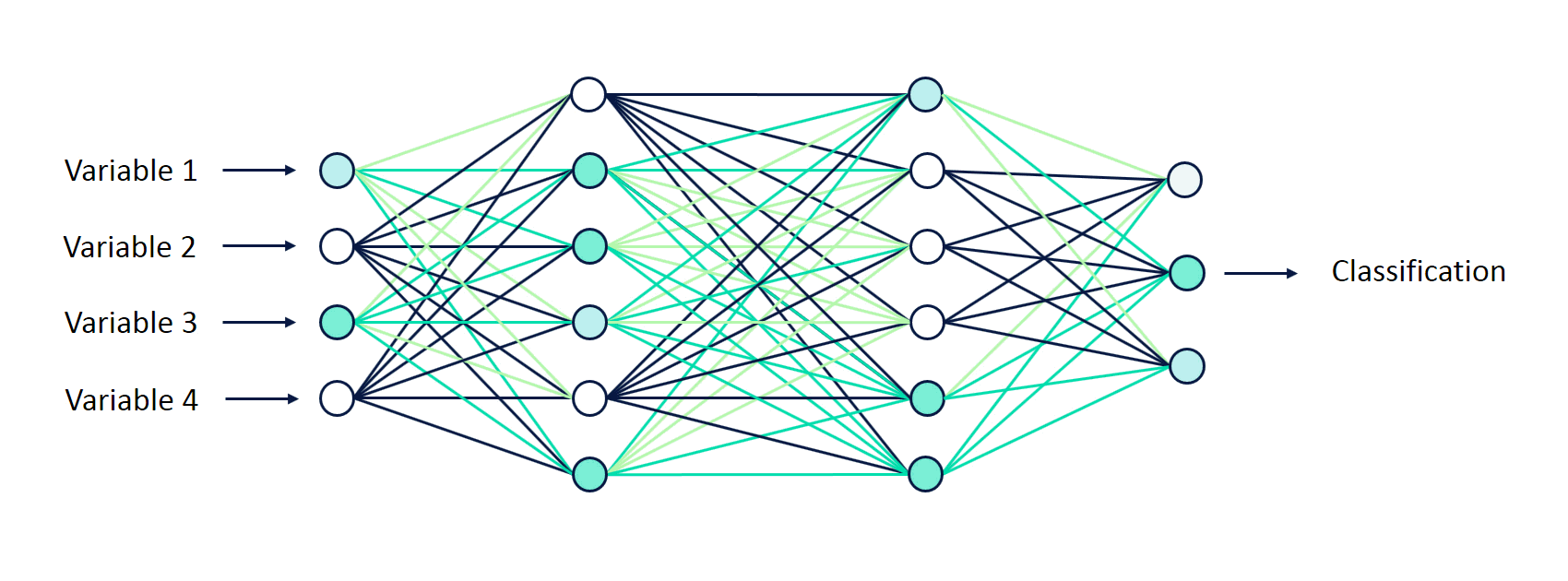
Um neurônio é essencialmente uma função cujas entradas são as saídas dos neurônios da camada anterior (ou as entradas da rede, no caso da camada de entrada da rede). A cada neurônio é associado um vetor de pesos, que pondera cada valor de entrada. O processo de aprendizado de redes neurais consiste no ajuste dos pesos de cada neurônio de maneira iterativa.
O Perceptron é o modelo mais simples de uma rede neural, contando com apenas um neurônio.
De maneira simplificada, durante o processo de treinamento a informação pode fluir nos dois sentidos da rede. No processo de forward propagation os dados de entrada atravessam a rede através dos neurônios, gerando uma saída. Já no processo de backward propagation o resultado da rede é confrontado com o resultado esperado, obtendo-se um erro com base no qual os pesos dos neurônios vão sendo ajustados na ordem contrária.
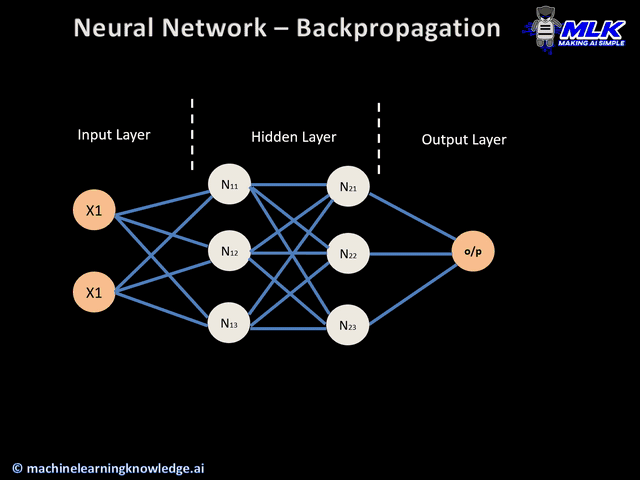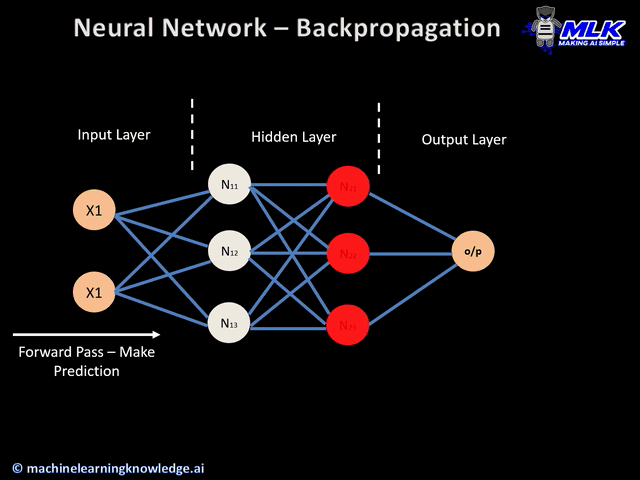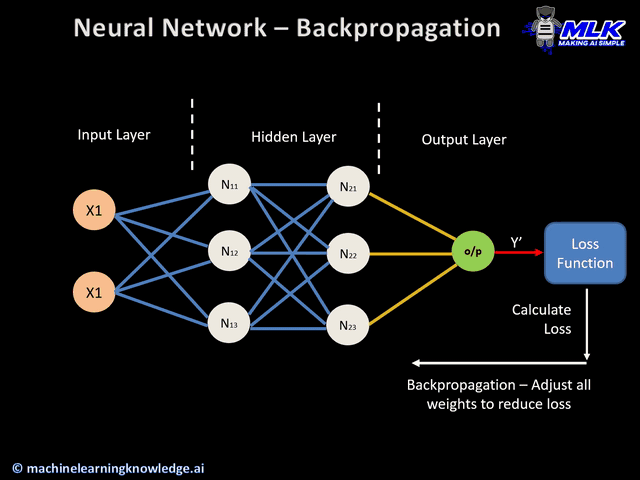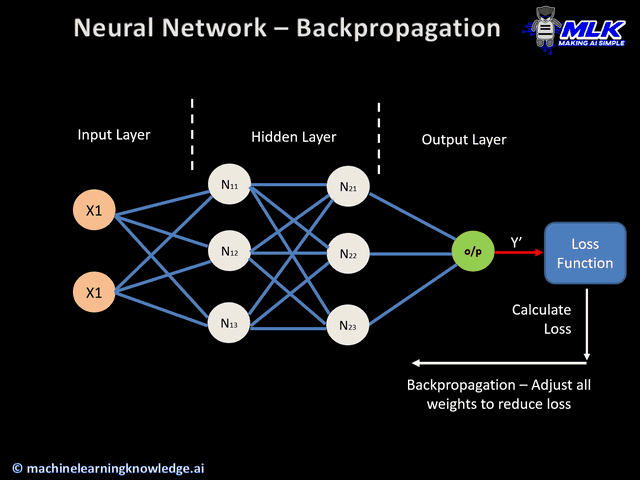
O processo de aprendizado se dá de forma iterativa, ajustando os pesos da rede de acordo com o erro cometido. Após aplicar um exemplo à rede, confronta-se o resultado obtido com o resultado esperado para o dado exemplo. Com base nisso os pesos na próxima iteração são dados pela seguinte expressão:
Onde é o fator de aprendizado, um parâmetro que controla o quão agressivos são os ajustes dos pesos da rede. Um fator de aprendizado alto aumenta a velocidade de convergência do algoritmo, porém aumenta a Probabilidade da convergência se dar em um ponto de mínimo local do erro, ou seja, as chances do ajuste ótimo de pesos ser encontrado diminui. Note que como as classes são dadas por ou , o ajuste só ocorre caso a classe predita seja diferente da classe verdadeira do exemplo.
A fórmula de ajuste dos pesos é obtida através do gradiente descendente, uma técnica de otimização que utiliza o Vetor gradiente para encontrar o mínimo local de uma função. A ideia é derivar o erro quadrático médio da previsão gerada pelo neurônio na direção de cada um dos pesos para obter o fator de ajuste de cada peso.