Integrais definidas

As integrais definidas são usadas para calcular a área sob o gráfico de uma função $f$ em um intervalo definido.
Imagine uma situação na qual desejamos calcular a área sob o gráfico de uma curva. Uma forma intuitiva de obter aproximações da área dessa curva é dividir o espaço sob a curva em vários retângulos como na figura:

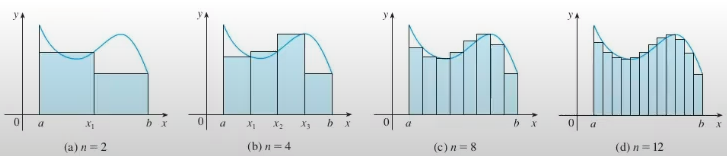
Assim, a soma das áreas desses diversos retângulos sob o gráfico de $f$ é uma aproximação da área sob o gráfico de $f$. Dessa forma, é possível deduzir que quanto mais retângulos mais precisa fica essa aproximação, pois sua base vai ficando cada vez mais estreita, até que quase não hajam “sobras”. Conhecendo o conceito de limites, podemos dizer então que a base dos triângulos tende a $0$, podemos dizer então que a soma da área desses retângulos (quase tão estreitos quanto linhas, ou seja: infinitamente estreitos) tende a ${\int }_a^{b}f(x)dx$, que representa a área sob o gráfico de $f$ ou seja:

$$\underset{\max \Delta x_i\to 0}{\lim }\sum _{i=1}^{n}f(c_i)\Delta x_i={\int }_a^{b}f(x)dx$$

Então, temos:

$${\int }_a^{b}f(x)dx=\text{aˊrea (com sinal) sob o graˊfico de f no intervalo }[a,b]$$

Propriedades

Podemos assumir algumas propriedades das integrais definidas:

$$\begin{array}{rl}& {\int }_a^b(f(x)+g(x))dx={\int }_a^{b}f(x)dx+{\int }_a^{b}g(x)dx\\ & {\int }_a^{b}k\cdot f(x)dx=k\cdot {\int }_a^{b}f(x)dx\\ & {\int }_a^{c}f(x)dx+{\int }_c^{b}f(x)dx={\int }_a^{b}f(x)dx\\ & \text{se }f(x)\le g(x)\text{, para todo }x\in [a,b]\text{, enta˜o}{\int }_a^{b}f(x)dx\le {\int }_a^{b}g(x)dx\end{array}$$

Existem ainda algumas convenções úteis da notação de integrais definidas, essas propriedades não partem de nenhuma definição, portanto são apenas convenções para facilitar o uso das integrais.

$$\begin{array}{rl}& {\int }_a^{a}f(x)dx=0\\ & {\int }_b^{a}f(x)dx=-{\int }_a^{b}f(x)dx\end{array}$$

É possível ainda definir o Teorema do valor médio para integrais, que fornece a seguinte definição:

Se $f$ é contínua no intervalo $[a,b]$, existe $c\in [a,b]$ tal que

$${\int }_a^{b}f(x)dx=f(c)\cdot (b-a)$$

Teorema fundamental do cálculo

A expressão que define as integrais definidas é capaz de sintetizar de forma muito eficiente (e elegante) o que de fato a integral definida representa, porém não é viável aplicá-la para resolução de problemas. Com o propósito de fornecer um meio para calcular as integrais definidas, surge então o Teorema fundamental do cálculo.
De forma geral, esse teorema serve para conectar a definição de integral definida com o cálculo das funções primitivas, nos permitindo utilizar as técnicas de integração no cálculo de áreas sob o gráfico de funções.

Teorema fundamental do cálculo - primeira versão
Seja $f$ uma função contínua no intervalo $[a,b]$. Para cada $x\in [a,b]$:

$$\phi (x)={\int }_a^{x}f(t)dt$$

então:

$${\phi }^{\prime }(x)=f(x),\forall x\in [a,b]$$

Teorema fundamental do cálculo - segunda versão
Sendo $f$ uma função contínua no intervalo $[a,b]$,

$$\text{se }\int f(x)dx=F(x)+C\text{enta˜o}{\int }_a^{b}f(x)dx=F(b)-F(a)$$