Método dos Trapézios

O método dos trapézios é utilizado para fazer a Integração numérica de funções. Esse método consiste em aproximar a função através de um polinômio de grau $1$ para então obter a área do gráfico da função aproximada.

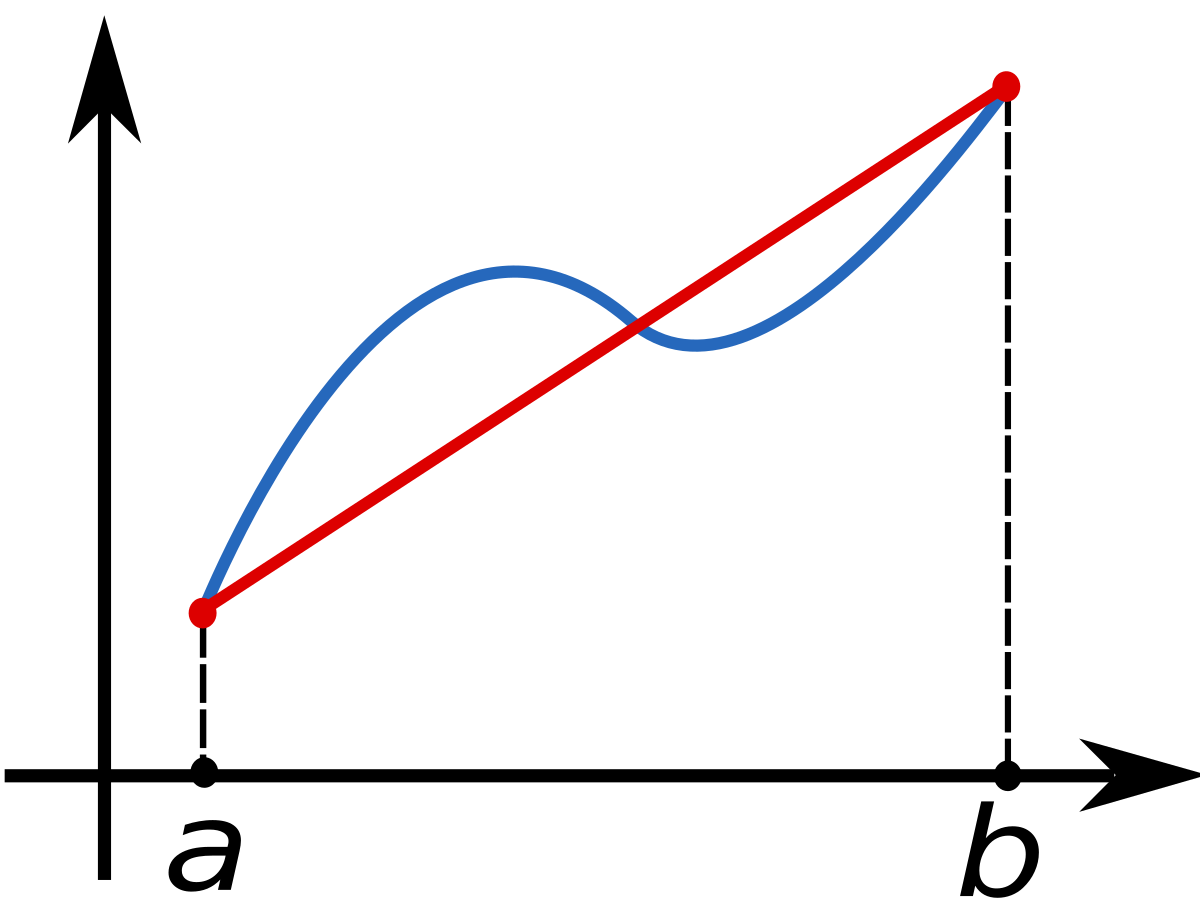
Dada uma função $f(x)$, é possível aproximar sua integral definida em um intervalo $[a,b]$ através da seguinte definição:

${\int }_{x_0}^{x_1}dx\approx h\frac{f(x_0)+f(x_1)}{2}$

com $x_0=a$ e $x_1=b$.

Vale notar que esse método produz resultados exatos caso $f$ seja uma função linear. Caso contrário, o limitante superior para o erro da aproximação é dado pela seguinte expressão:

$|E|\le \frac{h^3}{12}\max (|f^{(2)}(x)|,x\in [a,b])$

onde $h=b-a$.

O método pode ser implementado em python de uma maneira relativamente simples:

import numpy as np
 
 
def trapezio(i, f):
    h = i[1] - i[0]
 
    return h * ((f(i[0]) + f(i[1])) / 2)
 
 
i = [0, 2]
f = lambda x: np.exp(x)
 
print(trapezio(i, f))

É possível ainda subdividir o intervalo de integração e aplicar o método para cada um dos subintervalos, gerando uma aproximação mais precisa principalmente no caso do intervalo de integração ser muito grande. Dessa forma, o método dos trapézios repetidos para $n$ subintervalos é definido por:

${\int }_{x_0}^{x_n}dx\approx \frac{h}{2}(f(x_0)+2f(x_1)+\cdots +2f(x_{n-1})+f(x_n))$

O limitante superior para o erro da aproximação é dado pela soma dos erros obtidos em cada subintervalo, dessa forma, para $n$ subintervalos:

$|E|\le \frac{h^3}{12}\max (|f^{(2)}(x)|,x\in [a,b])$

onde $h=\frac{b-a}{n}$.

O método dos trapézios repetidos pode ser implementado em python da seguinte forma:

import numpy as np
 
 
def trapezio(i, f, n):
    x, h = np.linspace(i[0], i[1], num=n + 1, retstep=True)
    sum = f(x[0]) + f(x[n])
 
    for i in range(1, n):
        sum = sum + (2 * f(x[i]))
 
    return (h / 2) * sum
 
 
i = [0, 6]
f = lambda x: np.cos(4 * x)
 
 
print(trapezio(i, f, 14))