Volume de um sólido por fatiamento

Para calcular o volume de um sólido por fatiamento usamos uma ideia muito similar a usada para compreender as integrais definidas (tanto que usamos essas integrais nesse contexto). Se desejamos calcular o volume de um sólido em um intervalo $[a,b]$, devemos primeiro calcular a área de uma “fatia” que representa uma das secções transversais desse sólido, como mostra a figura:

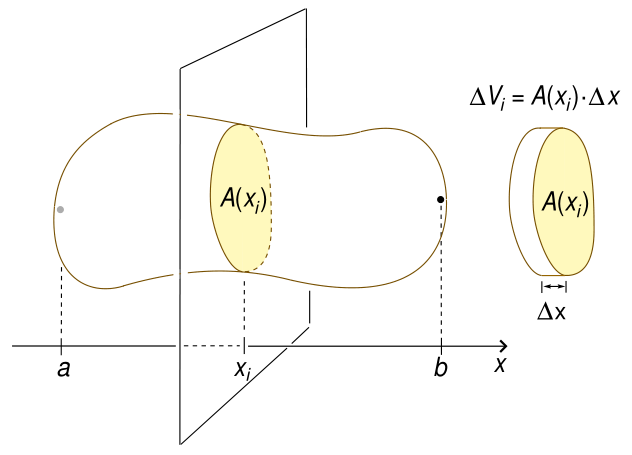
Semelhante a conceito dos retângulos ao calcular a área sob o gráfico de uma função, aqui multiplicamos a área dessa secção transversal por um $\Delta x$, que tende a $0$, ou seja, tem um comprimento ‘infinitesimal’. Dessa forma, obtemos o volume dessa fatia, agora basta somar o volume de todas essas fatias que compõe o sólido em todo o intervalo $[a,b]$ e obteremos o seu volume total.
Não podemos nos esquecer, porém, que a área é uma função de $x$, dessa forma o volume do sólido em um intervalo $[a,b]$ é dado por:

$$V={\int }_a^{b}A(x)dx$$