Cônicas

Sejam duas retas $e$ e $g$ concorrente em um ponto $O$ e não perpendiculares. Se mantermos a reta $e$ fixa e girarmos $g$ $360^{\circ }$ em torno de $e$ mantendo constante o ângulo entre as retas, obteremos uma superfície cônica circular infinita formada por duas folhas separadas pelo vértice $O$.

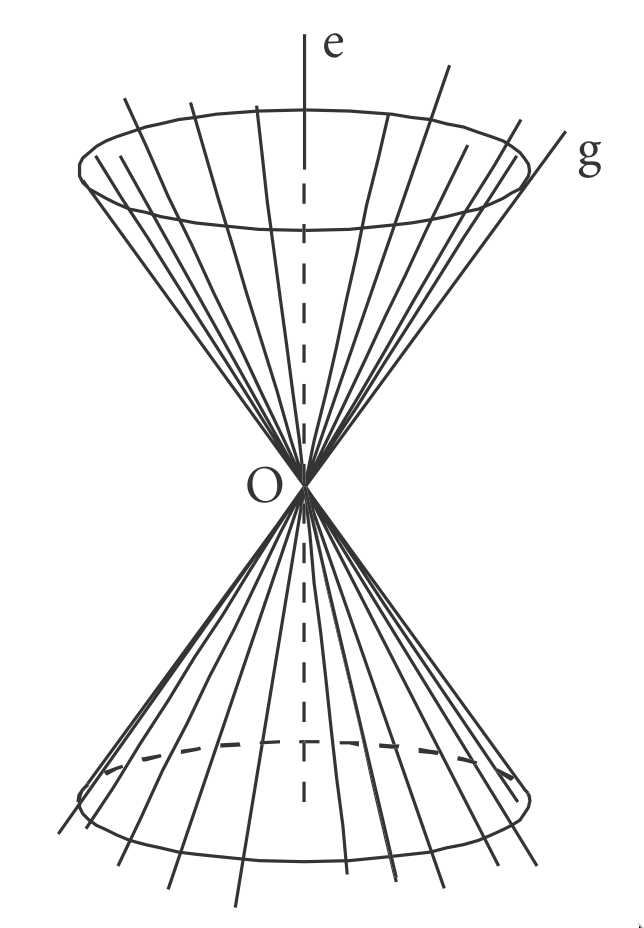
Nesse caso reta $g$ é a geratriz da superfície cônica, e a reta $e$ é o eixo da superfície.

Secção cônica, ou simplesmente cônica, é o conjunto de pontos que formam a intersecção de um plano $\pi$ com a superfície cônica.

Os diferentes tipos de cônicas são classificados de acordo com a forma como o plano $\pi$ intersecta a superfície cônica.

Quando uma superfície cônica é seccionada por um plano $\pi$ que não passa pelo vértice $O$, a cônica será:

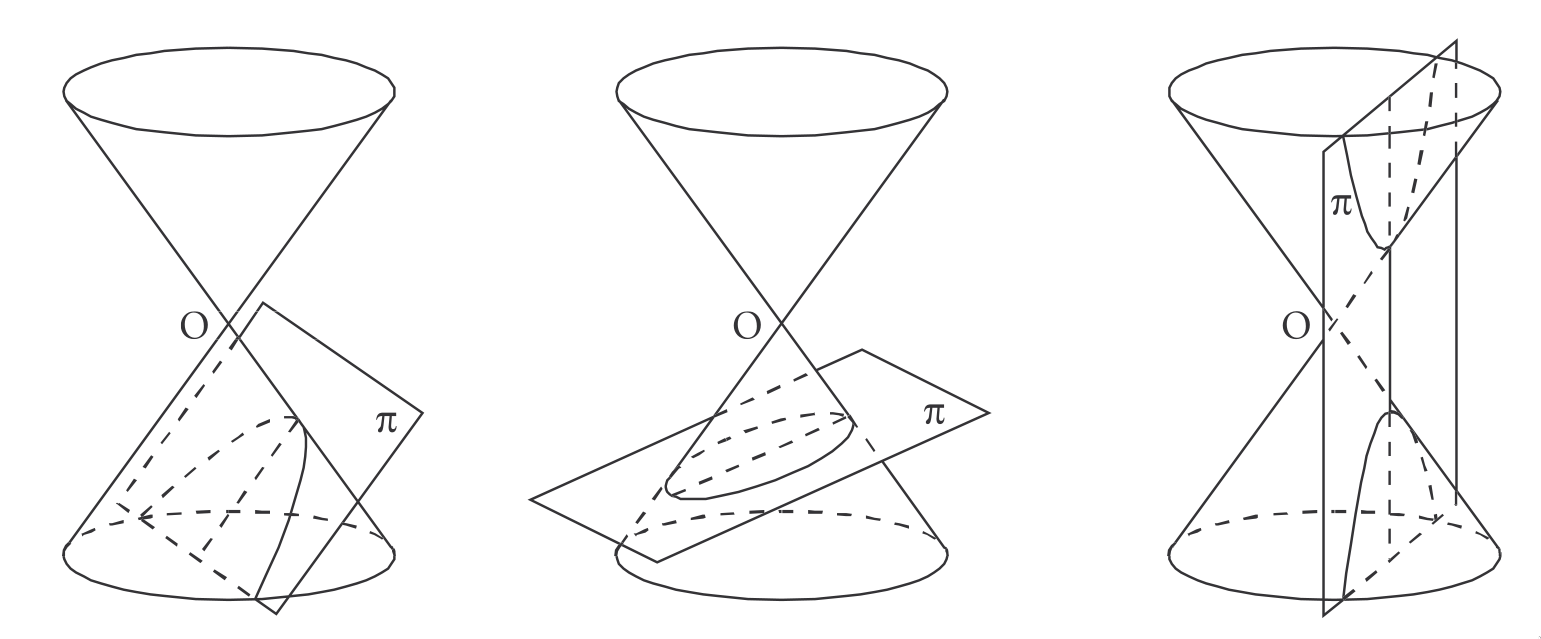
• uma parábola, se $\pi$ for paralelo a uma geratriz da superfície.
• uma elipse, se $\pi$ não for paralelo a uma geratriz e intercepta apenas uma das folhas da superfície (ou uma circunferência, se $\pi$ for perpendicular ao eixo).
• uma hipérbole, se $\pi$ não for paralelo a uma geratriz e interceptar as duas folhas da superfície. A hipérbole deve ser interpretada como uma curva só, constituída de dois ramos, um em cada folha da superfície.

Note que se os planos secantes passarem pelo vértice $O$, serão obtidas as chamadas cônicas “degeneradas”.

Quando uma superfície cônica é seccionada por um plano $\pi$ que passa pelo vértice $O$, a cônica será:

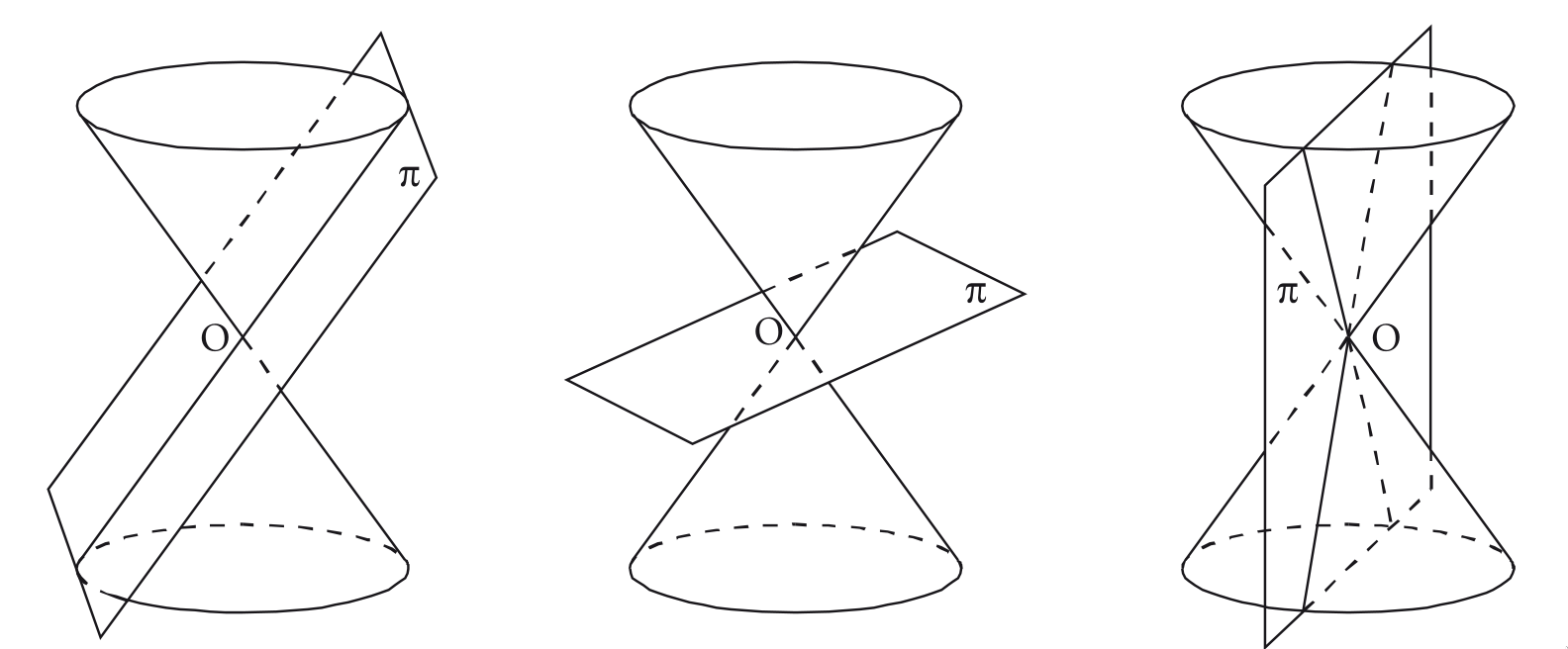
• uma reta, se $\pi$ for paralelo a uma geratriz da superfície.
• um ponto, se $\pi$ não for paralelo a uma geratriz e intercepta apenas uma das folhas da superfície.
• duas retas, se $\pi$ não for paralelo a uma geratriz e interceptar as duas folhas da superfície.

Equação geral

De maneira geral, uma cônica pode ser expressa por uma equação geral no seguinte formato:

$$A{x}^2+Bxy+C{y}^2+Dx+Ey+F=0$$

Dessa forma, é possível definir uma cônica com cinco pontos no plano, ou seja, por qualquer conjunto de cinco pontos do plano sempre passa uma única curva cônica.

Dados cinco pontos no plano $P_1(x_1,y_1)$, $P_2(x_2,y_2)$, $P_3(x_3,y_3)$, $P_4(x_4,y_4)$ e $P_5(x_5,y_5)$, basta substituir as coordenadas de cada ponto na equação geral, obtendo-se assim um sistema de equação linear com cinco equações e seis incógnitas:

$$\{\begin{array}{l}A{x}_1^2+B{x}_1{y}_1+C{y}_1^2+D{x}_1+E{y}_1+F=0\\ \\ A{x}_2^2+B{x}_2{y}_2+C{y}_2^2+D{x}_2+E{y}_2+F=0\\ \\ A{x}_3^2+B{x}_3{y}_3+C{y}_3^2+D{x}_3+E{y}_3+F=0\\ \\ A{x}_4^2+B{x}_4{y}_4+C{y}_4^2+D{x}_4+E{y}_4+F=0\\ \\ A{x}_5^2+B{x}_5{y}_5+C{y}_5^2+D{x}_5+E{y}_5+F=0\end{array}$$

Em seguida, pode-se resolver o sistema utilizando Gauss-Jordan. A solução desse sistema terá um dos parâmetros livres, então basta fixar um valor para esse parâmetro para obter-se uma equação geral da cônica determinada pelos cinco pontos.

Equação reduzida

Dada a equação geral de uma cônica, podemos aplicar rotação e translação de eixos no sistema cartesiano com o objetivo de simplificar essa equação.
Primeiro aplica-se a rotação com o objetivo de eliminar o termo misto $xy$. Após a rotação, a equação geral se transforma numa equação da seguinte forma:

$$A^{\prime }{x}^{\prime 2}+B^{\prime }{x}^{\prime }{y}^{\prime }+C^{\prime }{y}^{\prime 2}+D^{\prime }{x}^{\prime }+E^{\prime }{y}^{\prime }+F^{\prime }=0$$

onde:

$$\{\begin{array}{l}{A}^{\prime }=A{\cos }^2\theta +B\sin \theta \cos \theta +C{\sin }^2\theta \\ B^{\prime }=(C-A)\sin 2\theta +B\cos 2\theta \\ C^{\prime }=A{\sin }^2\theta -B\sin \theta \cos \theta +C{\cos }^2\theta \\ D^{\prime }=D\cos \theta +E\sin \theta \\ E^{\prime }=E\cos \theta -D\sin \theta \\ F^{\prime }=F\end{array}$$

O objetivo aqui é eliminar o termo misto da equação geral, portanto precisamos obter um ângulo de rotação $\theta$ que possibilite $B^{\prime }=0$. Após obter $B^{\prime }=0$, devemos recalcular todos os coeficientes da equação com o ângulo de rotação adotado.

Para auxiliar nos cálculos, já existem algumas relações a serem utilizadas:

$$\sin 2\theta =\frac{|B|}{H}\cos 2\theta =\text{sign}\left(\frac{A-C}{B}\right)\frac{|A-C|}{H}$$

com

$$H=\sqrt{B^2+(A-C{)}^2}$$

A partir disso podemos obter os outros elementos usando as seguintes relações fundamentais:

$$\cos 2\theta =2{\cos }^2\theta -1{\sin }^2\theta +{\cos }^2\theta =1$$

Após a rotação de eixos, aplica-se, se necessária, uma translação de eixos completando os quadrados da expressão, com o objetivo de eliminar os termos lineares. Após esse processo, obtém-se uma equação reduzida da cônica que possibilitará a sua identificação.

Invariantes

Existem alguns elementos associados às cônicas que não se alteram independente de rotações ou translações, portanto eles nos permitem identificar características das cônicas com base apenas nos valores dos seus parâmetros.
Dada uma cônica de equação geral:

$$A{x}^2+Bxy+C{y}^2+Dx+Ey+F=0$$

Temos duas matrizes associadas à ela:

$$Q=\left[\begin{array}{cc}A& \frac{B}{2}\\ \frac{B}{2}& C\end{array}\right]M=\left[\begin{array}{ccc}A& \frac{B}{2}& \frac{D}{2}\\ \frac{B}{2}& C& \frac{E}{2}\\ \frac{D}{2}& \frac{E}{2}& F\end{array}\right]$$

E também um valor discriminante:

$$\Delta =B^2-4AC=-\frac{1}{4}\det (Q)$$

A partir dos valores de $\Delta$ e $\det (M)$ é possível classificar qualquer cônica dados apenas seus parâmetros, sem a necessidade de fazer rotações e translações para obter sua forma reduzida:

Se $\Delta <0$, então a cônica é uma elipse ou suas degenerações, sendo:

• uma elipse, se $\Delta <0$ e $\det (M)<0$
• um ponto, se $\Delta <0$ e $\det (M)=0$
• um conjunto vazio, se $\Delta <0$ e $\det (M)>0$

Se $\Delta >0$, então a cônica é uma hipérbole ou suas degenerações, sendo:

• uma hipérbole, se $\Delta >0$ e $\det (M)\ne 0$
• duas retas concorrentes, se $\Delta >0$ e $\det (M)=0$

Se $\Delta =0$, então a cônica é uma parábola ou suas degenerações, sendo:

• uma parábola, se $\Delta =0$ e $\det (M)\ne 0$
• uma única reta ou duas retas paralelas, se $\Delta =0$ e $\det (M)=0$