Elipse

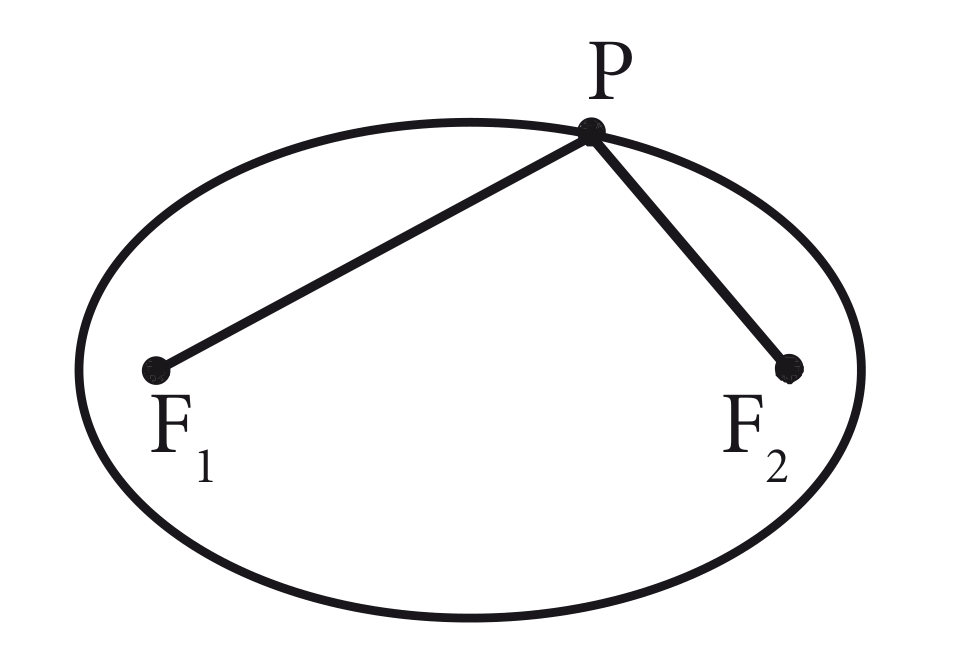
Elipse é o conjunto de todos os pontos de um plano cuja soma das distâncias a dois pontos fixos desse plano é constante.

Dados dois pontos distintos $F_1$ e $F_2$, tal que a distância $d(F_1,F_2)=2c$, e um número real positivo $a$ com $2a>2c$. Um ponto $P$ pertence à elipse se, e somente se:

$$d(P,F_1)+d(P,F_2)=2a$$

Elementos

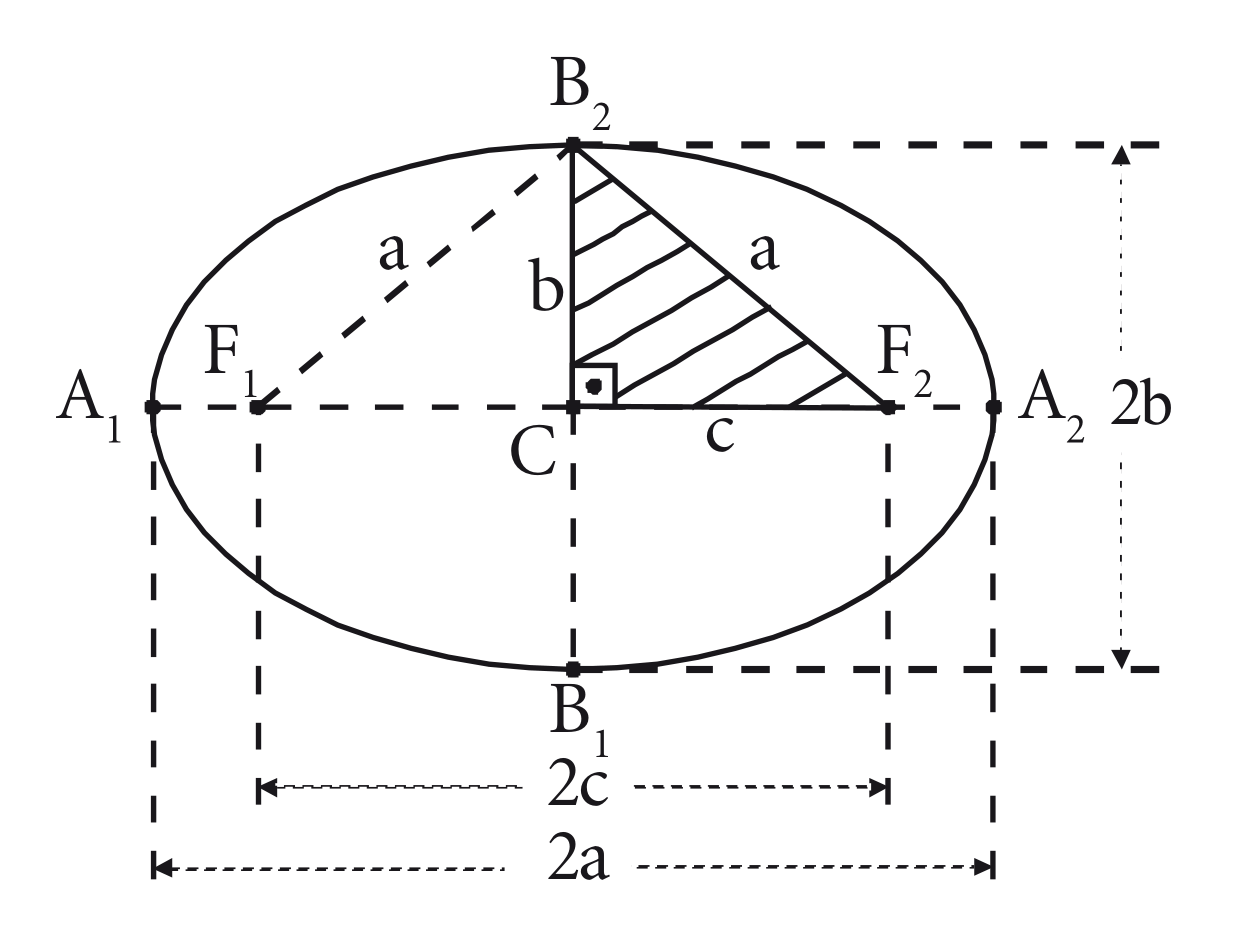
Com base na figura, uma elipse é composta pelos seguintes elementos:

• Focos: são os pontos $F_1$ e $F_2$.
• Distância focal: é a distância $2c$ entre os focos.
• Centro: é o ponto médio $C$ do segmento $F_1{F}_2$.
• Eixo maior: é o segmento $A_1{A}_2$ de comprimento $2a$ (esse segmento contém os focos).
• Eixo menor: é o segmento $B_1{B}_2$ de comprimento $2b$ e perpendicular a $A_1{A}_2$ no seu ponto médio.
• Vértices: são os pontos $A_1$, $A_2$, $B_1$ e $B_2$.

Pela figura, vê-se que é possível relacionar $a$, $b$ e $c$ através da seguinte equação:

$$a^2=b^2+c^2$$

Outro elemento importante é excentricidade da elipse, pois esse elemento indica forma da elipse. Elipses com excentricidade perto de $0$ são aproximadamente circulares, enquanto elipses com excentricidade mais próxima de $1$ são mais “achatadas”.

Excentricidade da elipse é o número real

$$e=\frac{c}{a}(0<e<1)$$

Equações reduzidas

Dada uma elipse de centro $C(0,0)$, levamos em conta dois casos distintos:

• O eixo maior está sobre o eixo dos $x$:

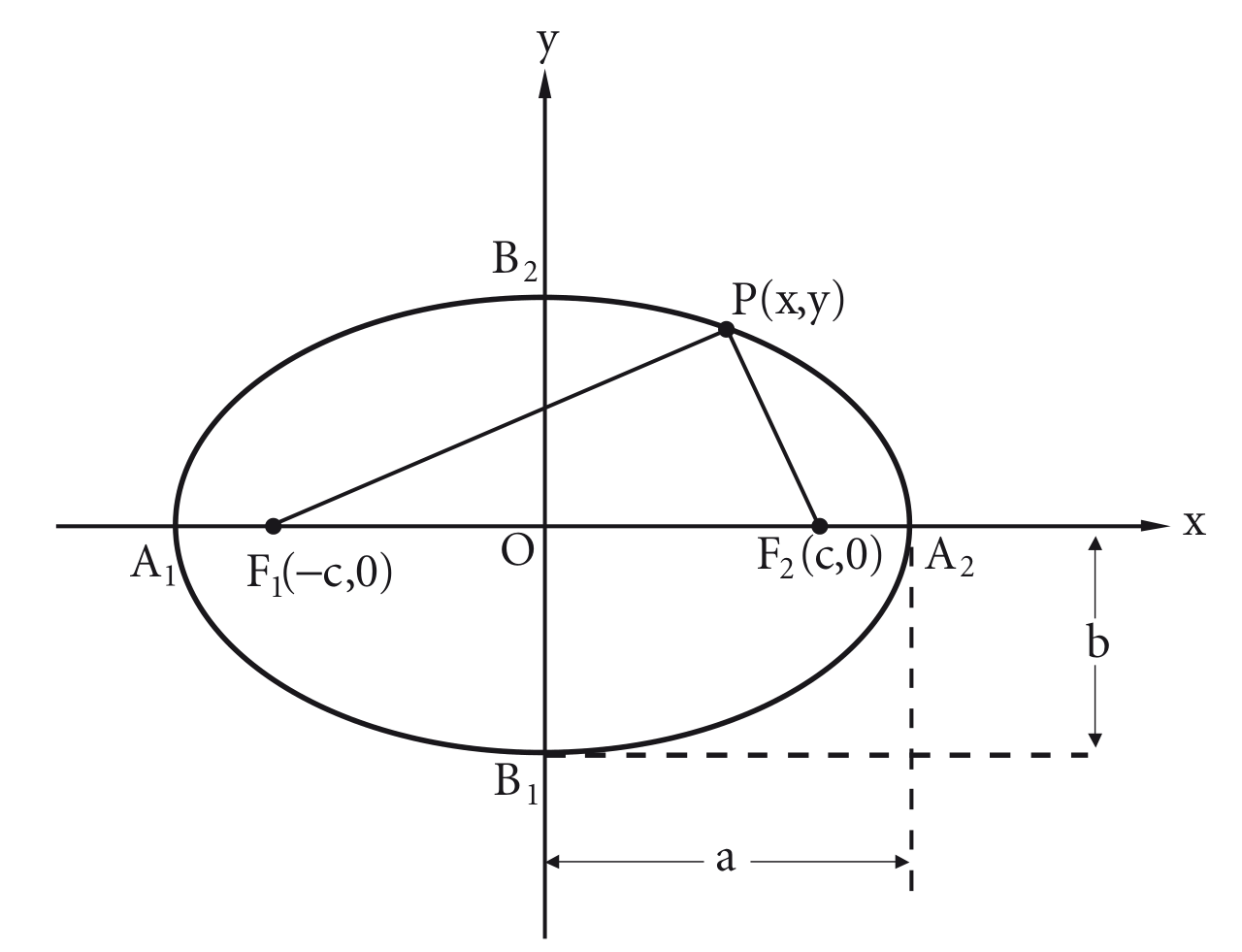
Dado um ponto $P(x,y)$ de uma elipse de focos $F_1(-c,0)$ e $F_2(c,0)$. Desenvolvendo a definição $d(P,F_1)+d(P,F_2)=2a$ obtém-se a equação reduzida para esse caso:

$$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$$

• O eixo maior está sobre o eixo dos $y$:

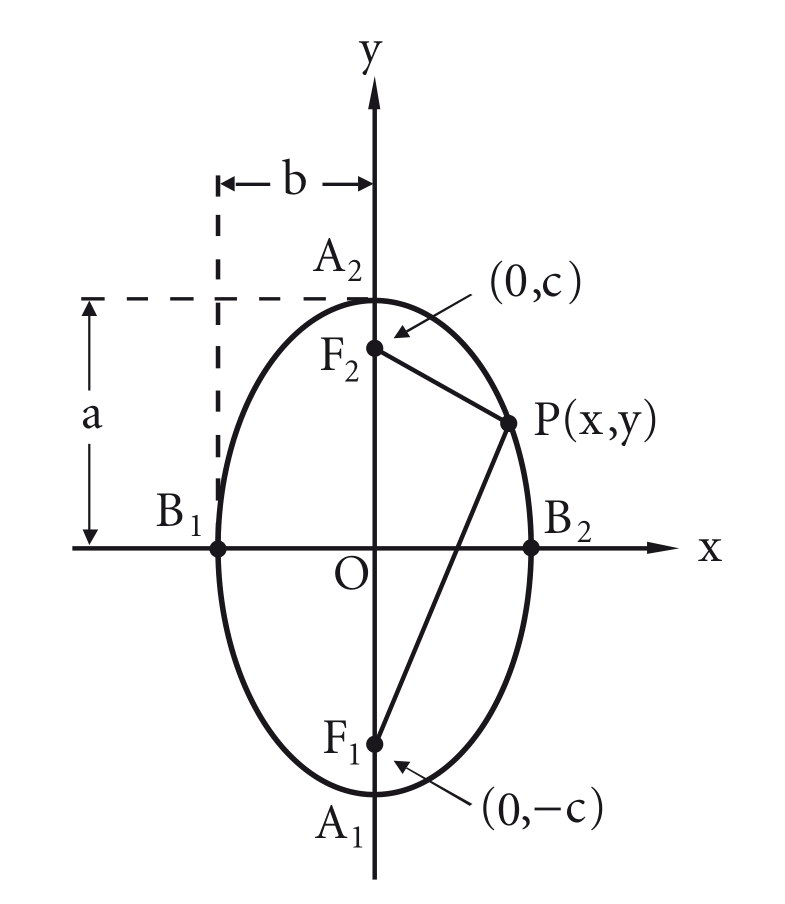
Dado um ponto $P(x,y)$ de uma elipse de focos $F_1(0,-c)$ e $F_2(0,c)$. Procedendo de maneira análoga ao caso anterior, obtém-se a seguinte equação reduzida:

$$\frac{x^2}{b^2}+\frac{y^2}{a^2}=1$$

Observação

Como em toda elipse tem-se $a>b$, para saber se a elipse tem seu eixo maior sobre o eixo $x$ ou $y$ basta observar onde está o maior denominador $a^2$ na sua equação reduzida, ou seja:

• Se $a^2$ for denominador de $x^2$, então o eixo maior está sobre o eixo $x$
• Se $a^2$ for denominador de $y^2$, então o eixo maior está sobre o eixo $y$

Translação de eixos

Usando a translação de eixos é possível manipular o centro da elipse para obter as equações reduzidas mesmo que o centro $C$ da elipse não seja o ponto $(0,0)$ do plano cartesiano.

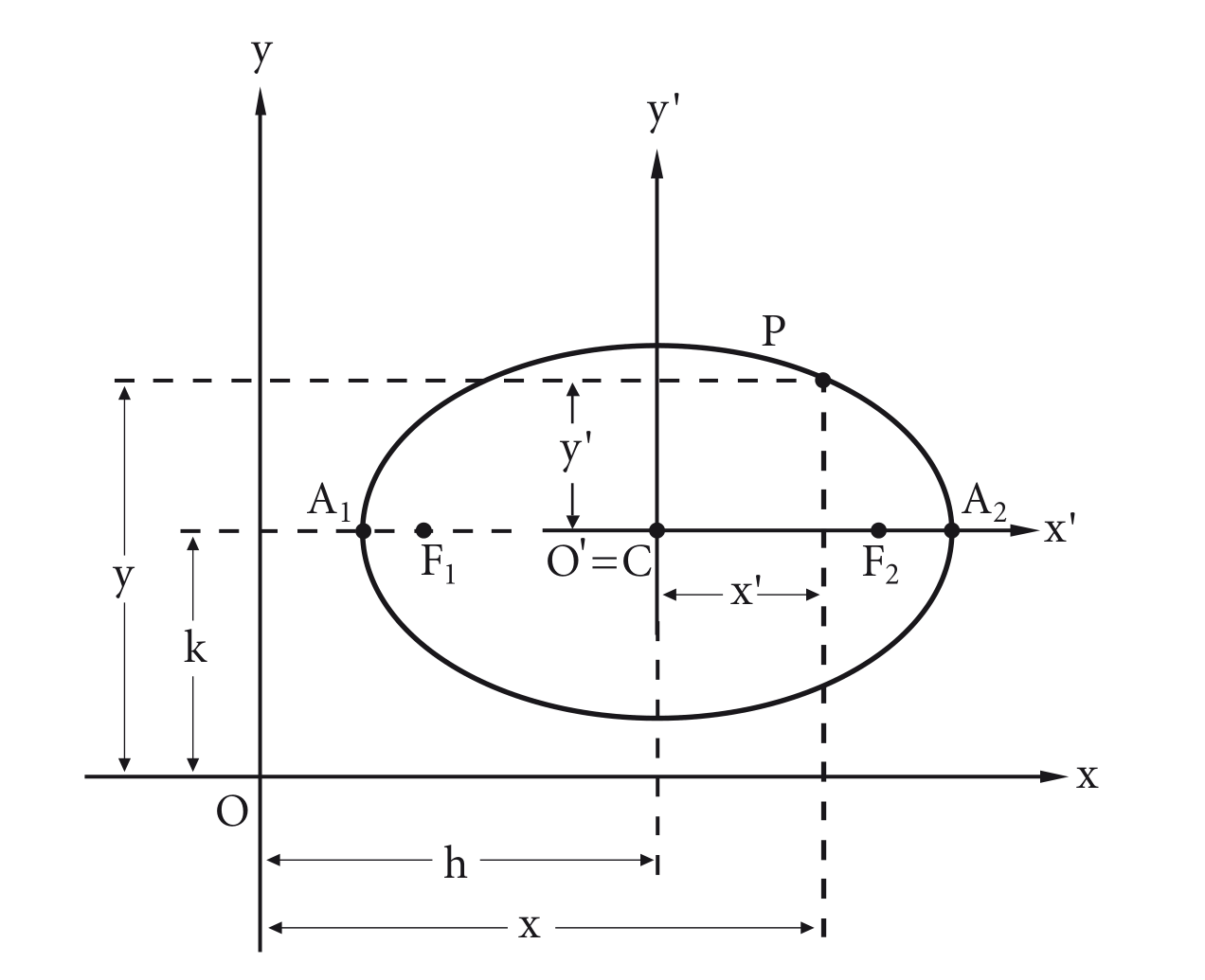
Dada uma elipse de centro $C=(h,k)\ne (0,0)$, temos dois casos possíveis para as equações reduzidas:

• O eixo maior é paralelo ao eixo dos $x$:

$$\frac{(x-h{)}^2}{a^2}+\frac{(y-k{)}^2}{b^2}=1$$

• O eixo maior é paralelo ao eixo dos $y$:

$$\frac{(x-h{)}^2}{b^2}+\frac{(y-k{)}^2}{a^2}=1$$

Equação geral

Eliminando os denominadores e desenvolvendo os quadrados de uma equação reduzida, obtemos uma equação geral da elipse, que tem a forma:

$$a{x}^2+b{y}^2+cx+dy+f=0$$

com $a$ e $b$ de sinais iguais.

Equações paramétricas

Dada uma elipse de equação $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$, podemos traçar uma circunferência de centro $O$ e raio igual ao semieixo maior da elipse e com base nessa circunferência obter as equações reduzidas da elipse.

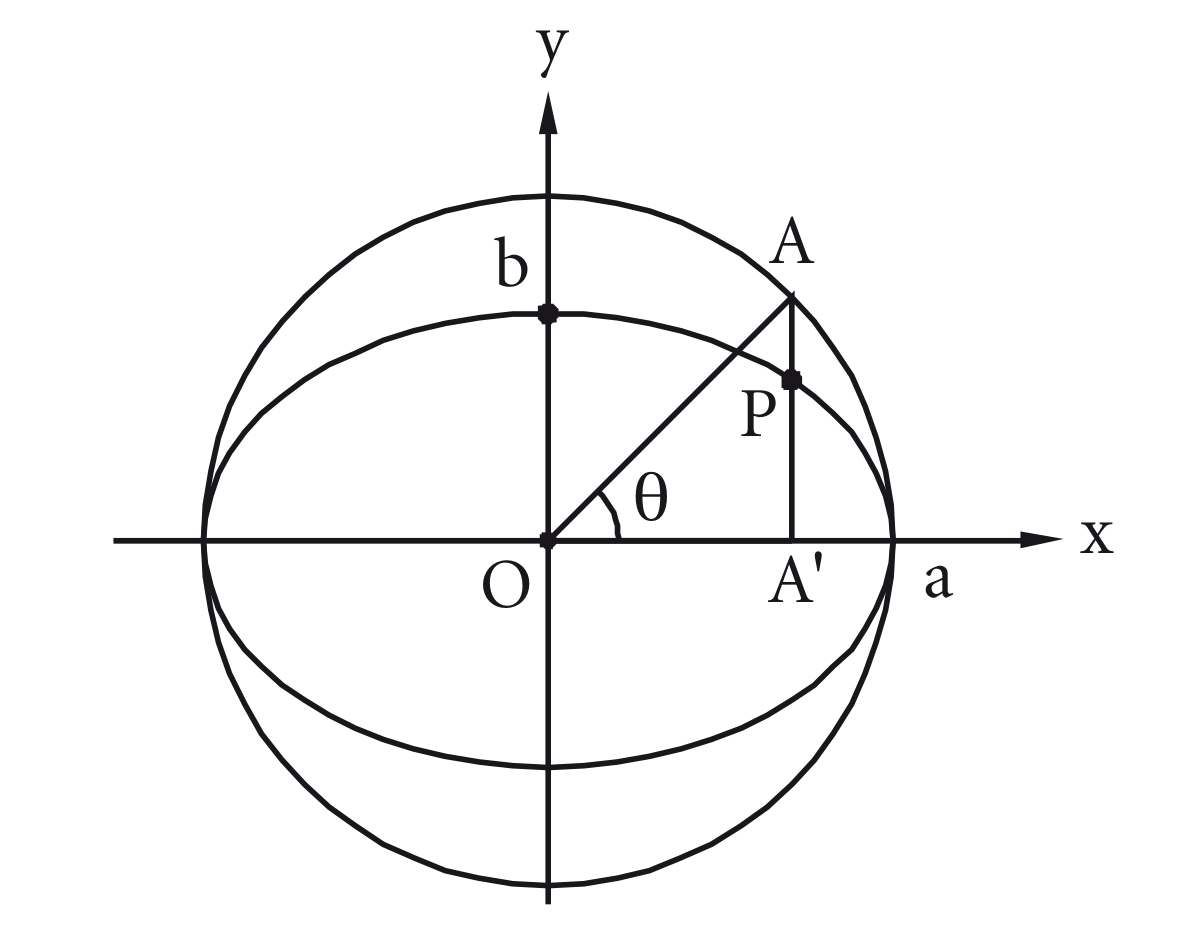
Dado um ponto $P(x,y)$ qualquer da elipse, temos dois casos possíveis para as equações paramétricas:

• O eixo maior é paralelo ao eixo dos $x$:

$$\{\begin{array}{l}x=a\cos \theta \\ y=b\sin \theta \end{array}0\le \theta \le 2\pi$$

• O eixo maior é paralelo ao eixo dos $y$:

$$\{\begin{array}{l}x=b\cos \theta \\ y=a\sin \theta \end{array}0\le \theta \le 2\pi$$

Vale destacar que quando o centro da elipse for $C(h,k)$, os dois casos possíveis para as equações tem a seguinte forma:

• O eixo maior é paralelo ao eixo dos $x$:

$$\{\begin{array}{l}x=h+a\cos \theta \\ y=k+b\sin \theta \end{array}0\le \theta \le 2\pi$$

• O eixo maior é paralelo ao eixo dos $y$:

$$\{\begin{array}{l}x=h+b\cos \theta \\ y=k+a\sin \theta \end{array}0\le \theta \le 2\pi$$