Variáveis aleatórias contínuas

A variável aleatória $X:\Omega \to \mathbb{R}$ é chamada de contínua quando seu conjunto imagem $Im(X)$ é infinito não-enumerável, ou seja, os possíveis valores de $X$ não podem ser descritos em forma de lista. Uma característica interessante desse tipo de variável aleatória é que não conseguimos atribuir probabilidade positiva para valores específicos, somente para intervalos de valores.

Função densidade de probabilidade

Quando lidamos com variáveis aleatórias contínuas, não podemos utilizar diretamente funções de distribuição de probabilidade, pois não é possível atribuir probabilidade positiva aos pontos. Ao invés disso, usamos funções de densidade de probabilidade para caracterizar as variáveis aleatórias contínuas.
A função de densidade representa a variação das probabilidades durante o intervalo, mas a imagem na função de densidade de probabilidade NÃO é a probabilidade do evento naquele determinado ponto.
Sabendo disso, podemos dizer que a área sob a curva da função de densidade de probabilidade em um intervalo $[a,b]$ é igual a $P(a\le X\le b)$. Para encontrar a área sob uma curva devemos usar integrais, daí surge a seguinte definição:

Dado um experimento aleatório $\mathcal{E}$ com espaço de probabilidade $(\Omega ,\mathcal{F},\mathcal{P})$, seja $X:\Omega \to \mathbb{R}$ uma variável aleatória contínua com conjunto imagem $Im(X)$. A função $f_X:\mathbb{R}\to \mathbb{R}$ é uma * função densidade de probabilidade (f.d.p.)* quando:

1. $f_X$ é não-negativa, ou seja: $$
   f_X(x) \geq 0,\qquad \forall x \in \mathbb{R}

2. A área total sob a curva deve ser igual a 1, ou seja: $$ \int_{-\infty}^{+\infty}{f_X(x)}\,dx = 1

Assim, podemos dizer que as áreas sob a curva da função densidade associadas a intervalos reais representam a distribuição das probabilidades ao longo de tais intervalos. Disso podemos tirar conclusões importantes:

Dada uma variável aleatória contínua $X:\Omega \to \mathbb{R}$:

$$P(X=x_0)={\int }_{x_0}^{x_0}{f}_X(x)dx=0$$

E ainda, pela natureza das integrais, tomando dois números reais $a$ e $b$ com $a<b$ temos que:

$$P(a\le X\le b)=P(a<X\le b)=P(a\le X<b)=P(a<X<b)={\int }_a^b{f}_X(x)dx$$

Ou seja, a abertura do intervalo não importa na hora de calcular a probabilidade.

Distribuição uniforme

Dado um experimento aleatório $\mathcal{E}$ com espaço de probabilidade $(\Omega ,\mathcal{F},P)$, sendo $X:\Omega \to \mathbb{R}$ uma variável aleatória contínua com conjunto imagem $Im(X)$. Dizemos que $X$ tem distribuição uniforme no intervalo $[a,b]\subset \mathbb{R}$ quando $Im(X)=[a,b]$ e sua função densidade de probabilidade é dada por:

$$f_X(x)=\{\begin{array}{l}\frac{1}{b-a},\text{ se }x\in [a,b]\\ \\ 0,\text{caso contraˊrio.}\end{array}$$

A notação utilizada para esse tipo de distribuição é $X\sim Uniforme([a,b])$. Esse tipo de distribuição é utilizada em situações nas quais a probabilidade da variável aleatória pertencer a intervalos de tamanhos iguais é sempre a mesma.

Distribuição exponencial

Dado um experimento aleatório $\mathcal{E}$ com espaço de probabilidade $(\Omega ,\mathcal{F},P)$, sendo $X:\Omega \to \mathbb{R}$ uma variável aleatória contínua com conjunto imagem $Im(X)$. Dizemos que $X$ tem distribuição exponencial com parâmetro $\alpha$, $\alpha >0$ quando $Im(X)=]0,+\infty [$ e sua função densidade de probabilidade é dada por:

$$f_X(x)=\{\begin{array}{l}\alpha e^{-\alpha x}\text{ se }x>0\\ \\ 0,\text{caso contraˊrio.}\end{array}$$

A notação utilizada para esse tipo de distribuição é $X\sim Exponencial(\alpha )$. Esse tipo de distribuição é usado quando existe uma variação exponencial das probabilidades da variável aleatória. Vale destacar que o parâmetro $\alpha$ indica a taxa de ocorrência do evento por unidade de medida, que pode ser tempo, distância, volume etc.

Distribuição normal

Esse é o tipo de distribuição de variáveis aleatórias contínuas mais importante, pois ela é frequentemente uma ótima aproximação para a distribuição de diversas outras variáveis aleatórias contínuas. Geralmente utilizamos a distribuição normal na modelagem de medidas físicas de indivíduos (altura, peso, pressão sanguínea), medidas de clima, dimensões de produtos manufaturados e error de medições científicas.
Dado um experimento aleatório $\mathcal{E}$ com espaço de probabilidade $(\Omega ,\mathcal{F},P)$, sendo $X:\Omega \to \mathbb{R}$ uma variável aleatória contínua com conjunto imagem $Im(X)$. Dizemos que $X$ tem distribuição normal com parâmetros $\mu$ e ${\sigma }^2$, $\mu \in \mathbb{R}$ e ${\sigma }^2>0$, quando $Im(X)=\mathbb{R}$ e sua função densidade de probabilidade é dada por:

$$f_X(x)=\frac{1}{\sqrt{2\pi \sigma }}\exp \left(-\frac{(x-\mu {)}^2}{2{\sigma }^2}\right),\forall x\in \mathbb{R}$$

A notação utilizada para esse tipo de distribuição é $X\sim Normal(\mu ,{\sigma }^2)$. Nesse caso o parâmetro $\mu$ representa o valor médio da variável aleatória $X$, e o parâmetro $\sigma$ representa o desvio padrão da variável aleatória $X$ (o quando, em média, os possíveis valores da variável aleatória se distanciam do seu valor médio $\mu$).
Vale destacar que, pelo fato do gráfico dessa função ser simétrico, temos a seguinte identidade:

$$P(X>\mu +k)=P(X<\mu -k),\forall k\ge 0$$

O problema a princípio é que nesse caso $f_X(x)$ não possui solução analítica, então é necessário “normalizar” a função. Para isso é necessário transformar a variável $X$ em uma outra variável $Z$ tal que:

$$Z:=\frac{X-\mu }{\sigma }\sim Normal(0,1)$$

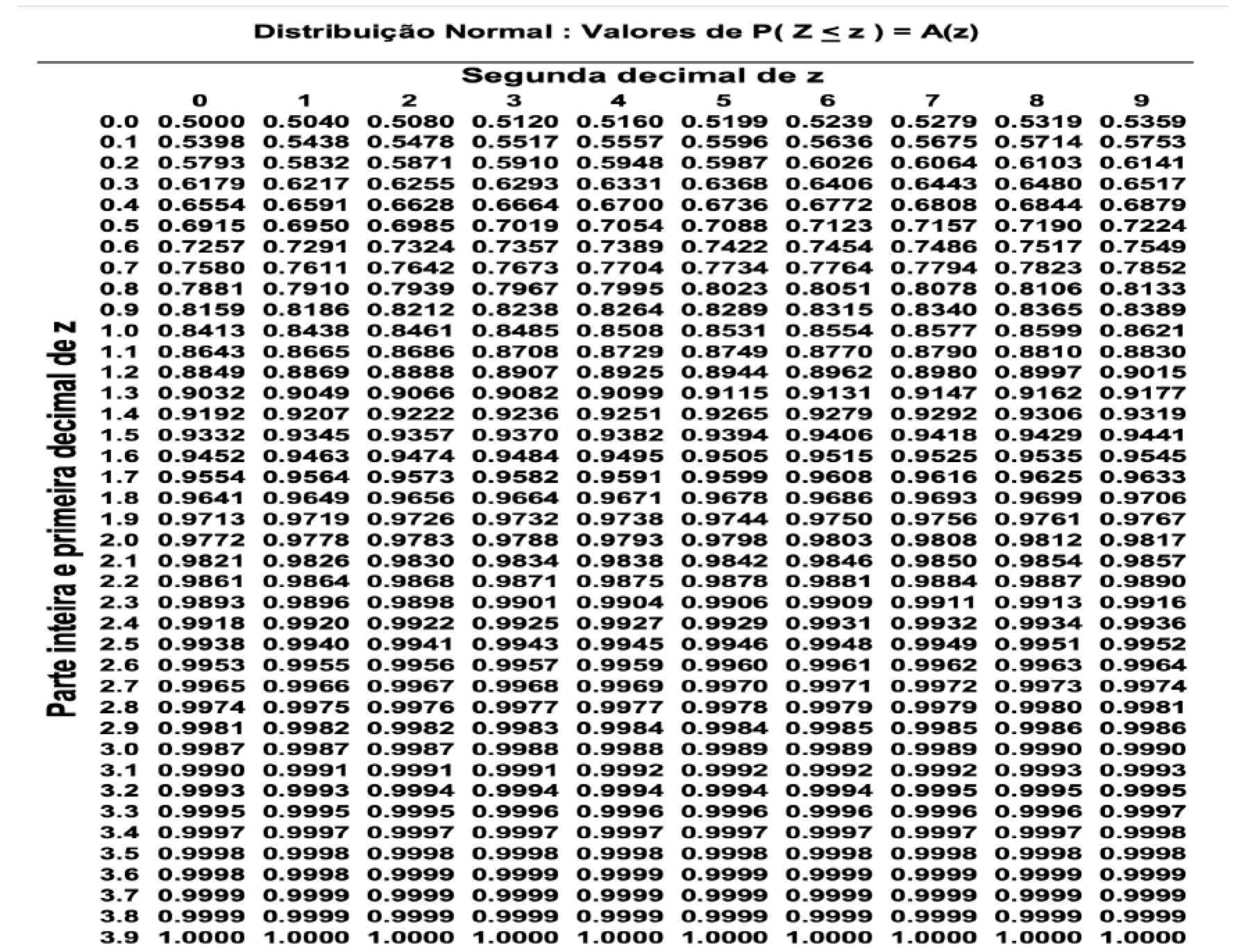
Assim, podemos reduzir o cálculo da probabilidade de um intervalo $[a,b]$ de qualquer variável aleatória com distribuição $X\sim Normal(\mu ,{\sigma }^2)$ ao cálculo da área da densidade $f_Z$, $Z\sim Normal(0,1)$ no intervalo padronizado $\left[\frac{a-\mu }{\sigma },\frac{b-\mu }{\sigma }\right]$. E é claro, as probabilidades para $f_Z$ estão tabeladas: