Parábola

Seja $d$ uma reta qualquer e $F$ um ponto não pertencente a $d$. Chamamos de parábola o conjunto de todos os pontos de um plano equidistantes do ponto $F$ e da reta $d$. Dessa forma, um ponto $P$ qualquer pertence à parábola se e somente se:

$$d(P,F)=d(P,d)$$

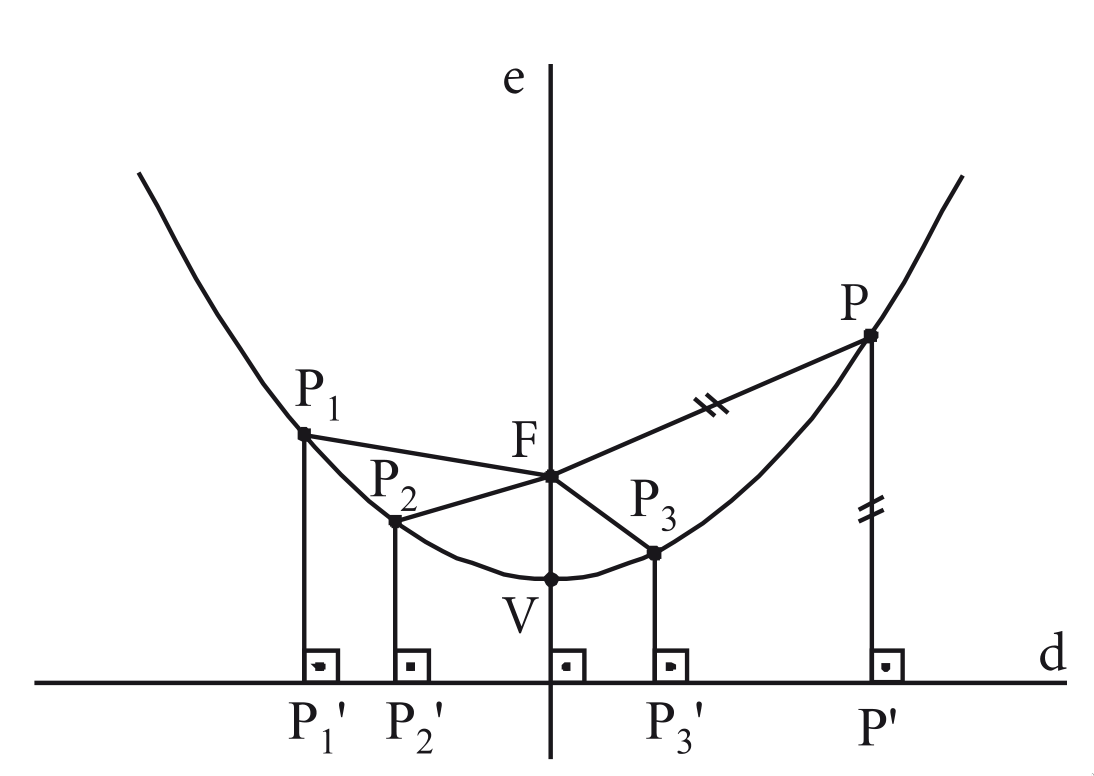
Alguns pontos e eixos notáveis das parábolas são:

• Foco: é o ponto $F$.
• Diretriz: é a reta $d$.
• Eixo: é a reta $e$ que passa por $F$ e é perpendicular a $d$.
• Vértice: é o ponto $V$ de intersecção da parábola com o seu eixo.

Equações reduzidas

Dada uma parábola de vértice $V(0,0)$, existem dois casos possíveis, note que em ambos os casos o número real $p\ne 0$ é chamado de parâmetro da parábola:

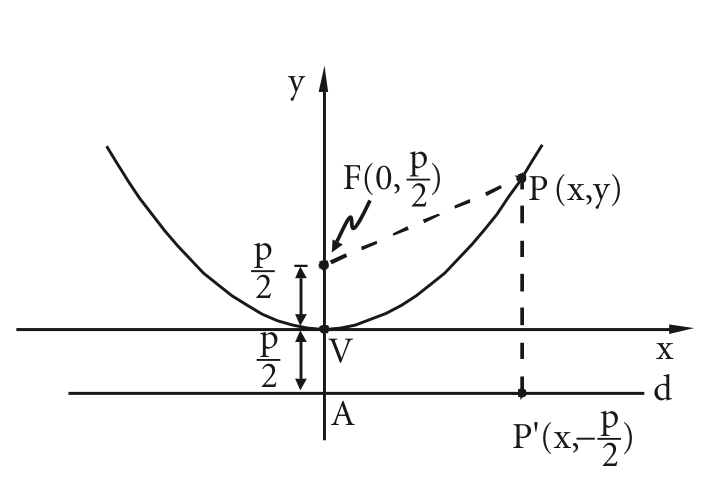
• Se o eixo da parábola é o eixo dos $y$:
  Seja $P(x,y)$ um ponto qualquer da parábola de foco $F(0,\frac{p}{2})$ e diretriz de equação $y=-\frac{p}{2}$
  A equação reduzida da parábola nesse caso é:

$$x^2=2py$$

Analisando a equação, pode-se perceber que $py\ge 0$, dessa forma seus sinais são sempre iguais. Temos então dois casos de sinais que influenciam na concavidade da parábola:

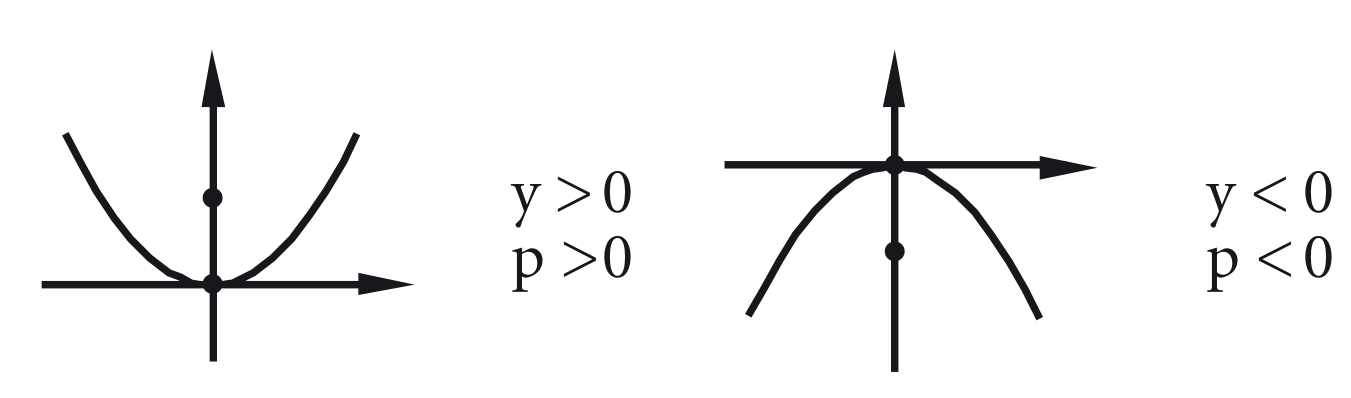
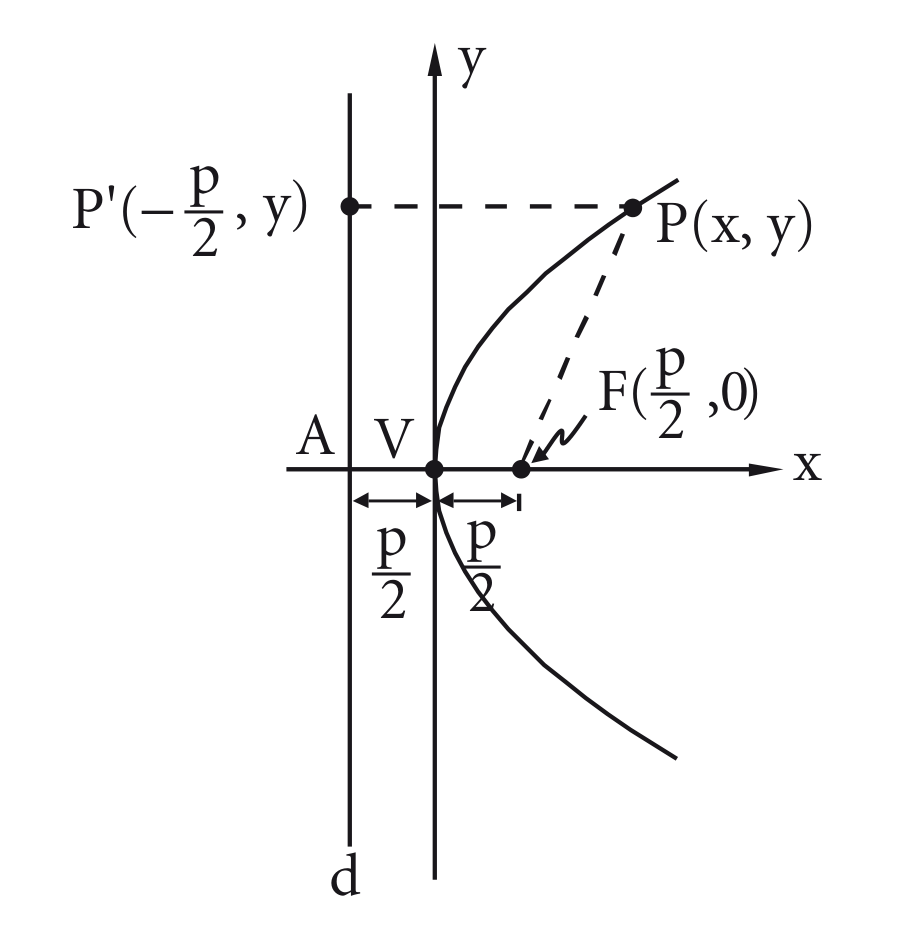
• Se o eixo da parábola é o eixo dos $x$:
  Seja $P(x,y)$ um ponto qualquer da parábola de foco $F(\frac{p}{2},0)$ e diretriz de equação $x=-\frac{p}{2}$
  A equação reduzida da parábola nesse caso é:

$$y^2=2px$$

Analisando a equação, pode-se perceber que $px\ge 0$, dessa forma seus sinais são sempre iguais. Temos então dois casos de sinais que influenciam na concavidade da parábola:

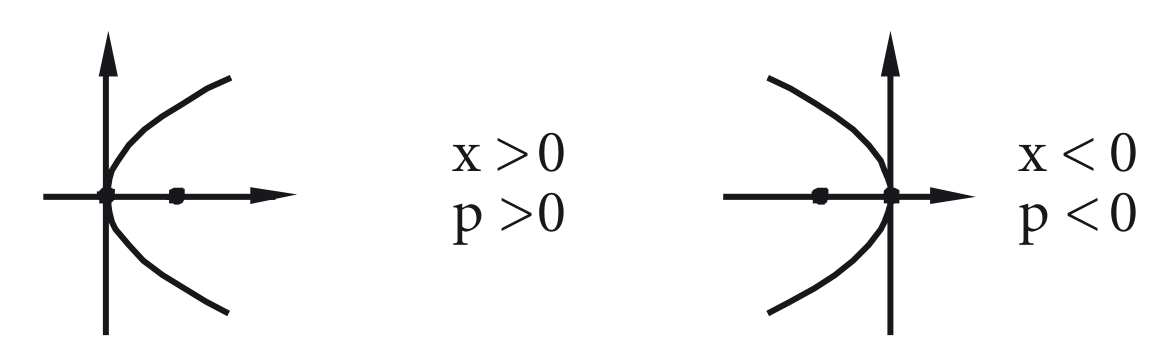
Translação de eixos

Usando a translação de eixos é possível manipular o vértice da parábola para obter as equações reduzidas mesmo que o vértice $V$ da parábola não seja o ponto $(0,0)$ do plano cartesiano.

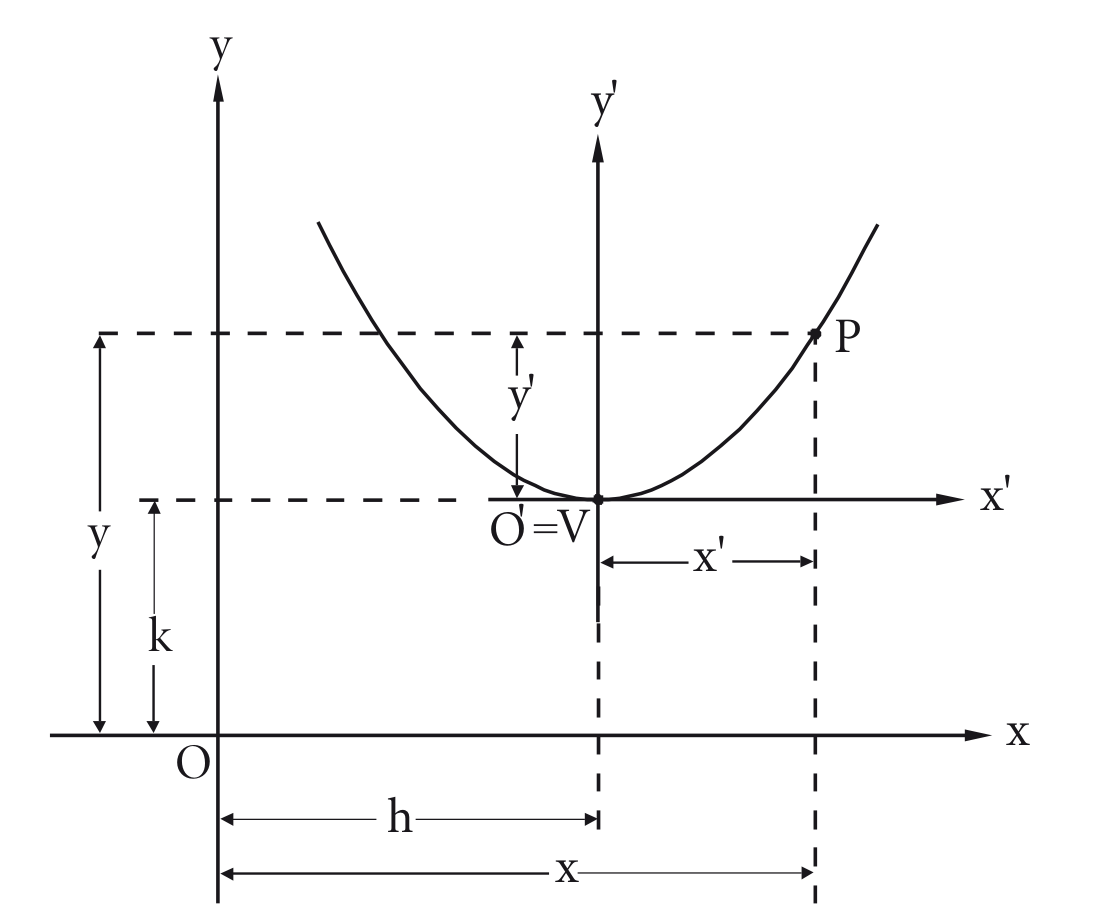
Dada uma parábola de vértice $V\ne (0,0)$, tomamos um novo sistema $x^{\prime }{O}^{\prime }{y}^{\prime }$ tal que $O^{\prime }=V$. Assim, ao escrever a equação reduzida da parábola em relação ao novo sistema, podemos substituir $x^{\prime }$ e $y^{\prime }$ pelas suas fórmulas de translação, obtendo as expressões:

• Se o eixo da parábola é paralelo ao eixo dos $y$:
  A equação na forma padrão da parábola nesse caso é:

$$(x-h{)}^2=2p(y-k)$$

• Se o eixo da parábola é paralelo ao eixo dos $x$:
  A equação na forma padrão da parábola nesse caso é:

$$(y-k{)}^2=2p(x-h)$$

Note que as observações sobre o sinal do parâmetro com relação à concavidade são válidas também para essas equações.

Equação geral

Tomando como base a equação da parábola na forma padrão, se apenas desenvolvermos o quadrado e as multiplicações chegaremos na equação geral da parábola, que apresenta duas possíveis formas:

$$a{x}^2+cx+dy+f=0a\ne 0$$

ou

$$b{y}^2+cy+dx+f=0b\ne 0$$

Equação explícita

Colocando o $x$ ou o $y$ em evidência em uma equação geral de uma parábola, obtemos sua forma reduzida. Existem duas possíveis formas para as equações reduzidas de uma parábola:

$$y=a{x}^2+bx+ca\ne 0$$

ou

$$x=a{y}^2+by+ca\ne 0$$

Equações paramétricas

Considerando as equações reduzidas da parábola, podemos trocar $x$ ou $y$ por um parâmetro $t\in \mathbb{R}$, dessa forma obtemos as equações paramétricas da parábola para cada caso:
Caso a equação reduzida da parábola seja $x^2=2py$:

$$\{\begin{array}{l}x=t\\ y=\frac{1}{2p}{t}^2\end{array}$$

Caso a equação reduzida da parábola seja $y^2=2px$:

$$\{\begin{array}{l}x=\frac{1}{2p}{t}^2\\ y=t\end{array}$$