Hipérbole é o conjunto de todos os pontos de um plano cuja diferença das distâncias, em valor absoluto, a dois pontos fixos desse plano é constante.
Dados dois pontos distintos e tal que a distância , e um número real positivo de modo que . Um ponto pertence à hipérbole se, e somente se:
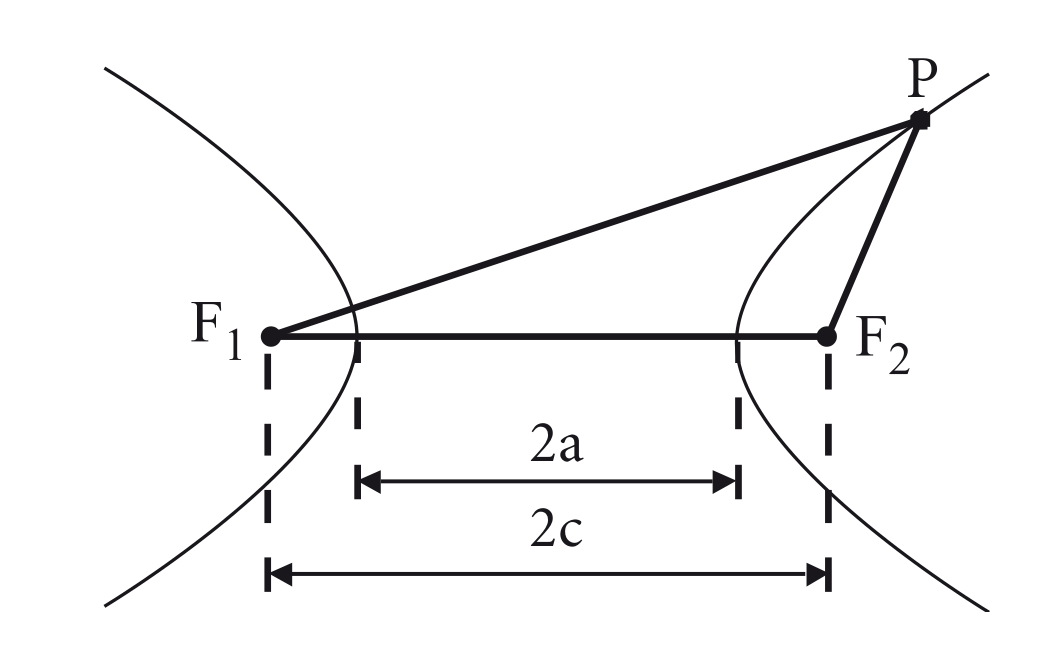
Elementos
Dados dois pontos quaisquer e , tal que . Chamando de o ponto médio do segmento , pode-se traçar uma circunferência de centro e raio .
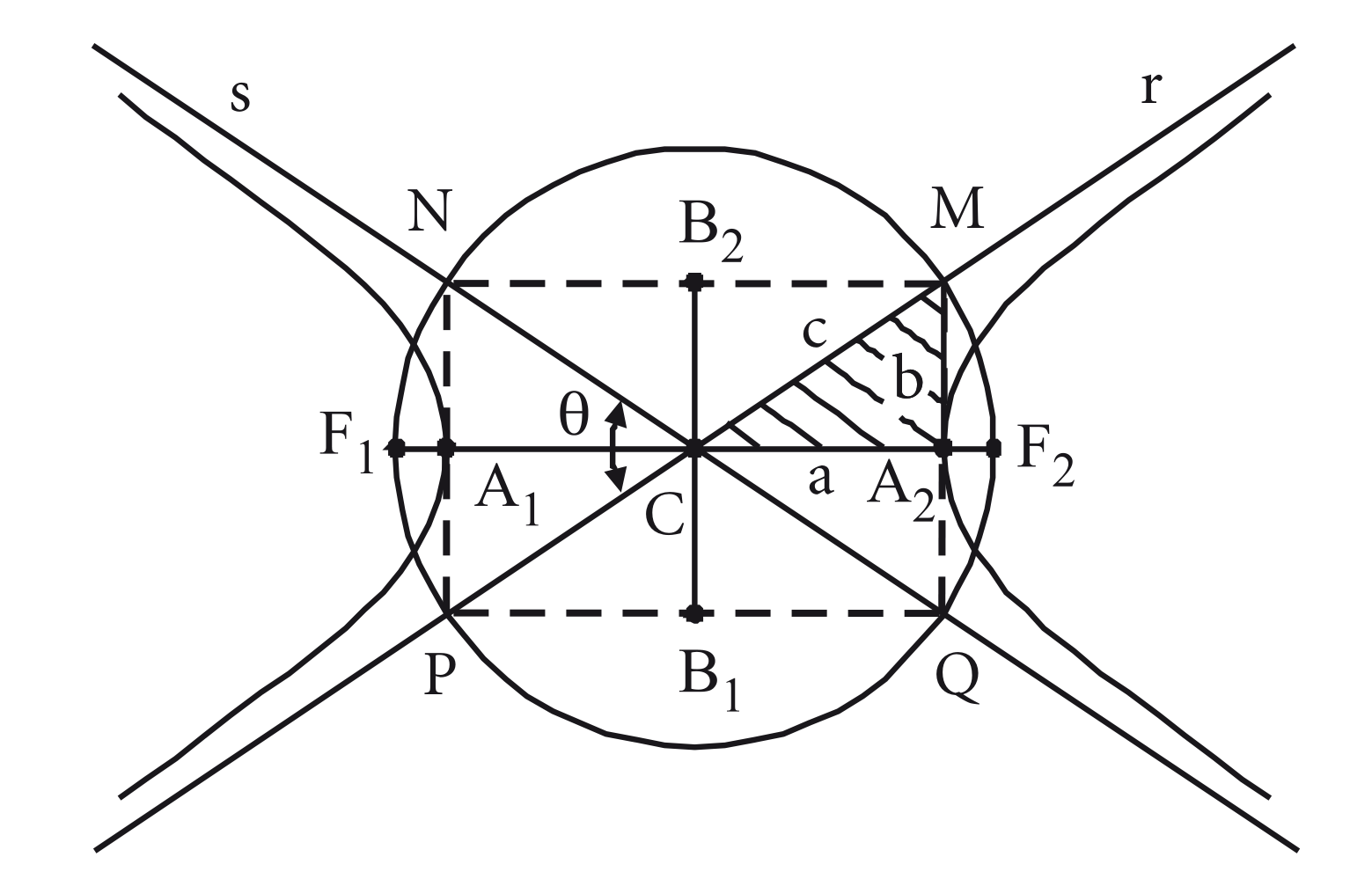
Com base na figura, uma hipérbole é composta pelos seguintes elementos:
- Focos: são os pontos e .
- Distância focal: é a distância entre os focos.
- Centro: é o ponto médio do segmento .
- Vértices: são os pontos e .
- Eixo real ou transverso: é o segmento de comprimento .
- Eixo imaginário ou não transverso: é o segmento de comprimento , com em .
- Assíntotas: são as retas e das quais a hipérbole se aproxima cada vez mais à medida que os pontos se afastam dos vértices.
Pela figura, vê-se que é possível relacionar , e através da seguinte equação:
Outro elemento importante é a excentricidade da hipérbole, definida por:
A excentricidade se relaciona diretamente com a abertura da hipérbole (denotada pelo ângulo na figura), quanto maior a excentricidade, maior a abertura da hipérbole. Quando , as assíntotas se tornam perpendiculares (). Nesse caso a hipérbole é chamada de hipérbole equilátera.
Equações reduzidas
Dada uma hipérbole de centro , existem dois casos distintos:
- O eixo real está sobre o eixo dos :
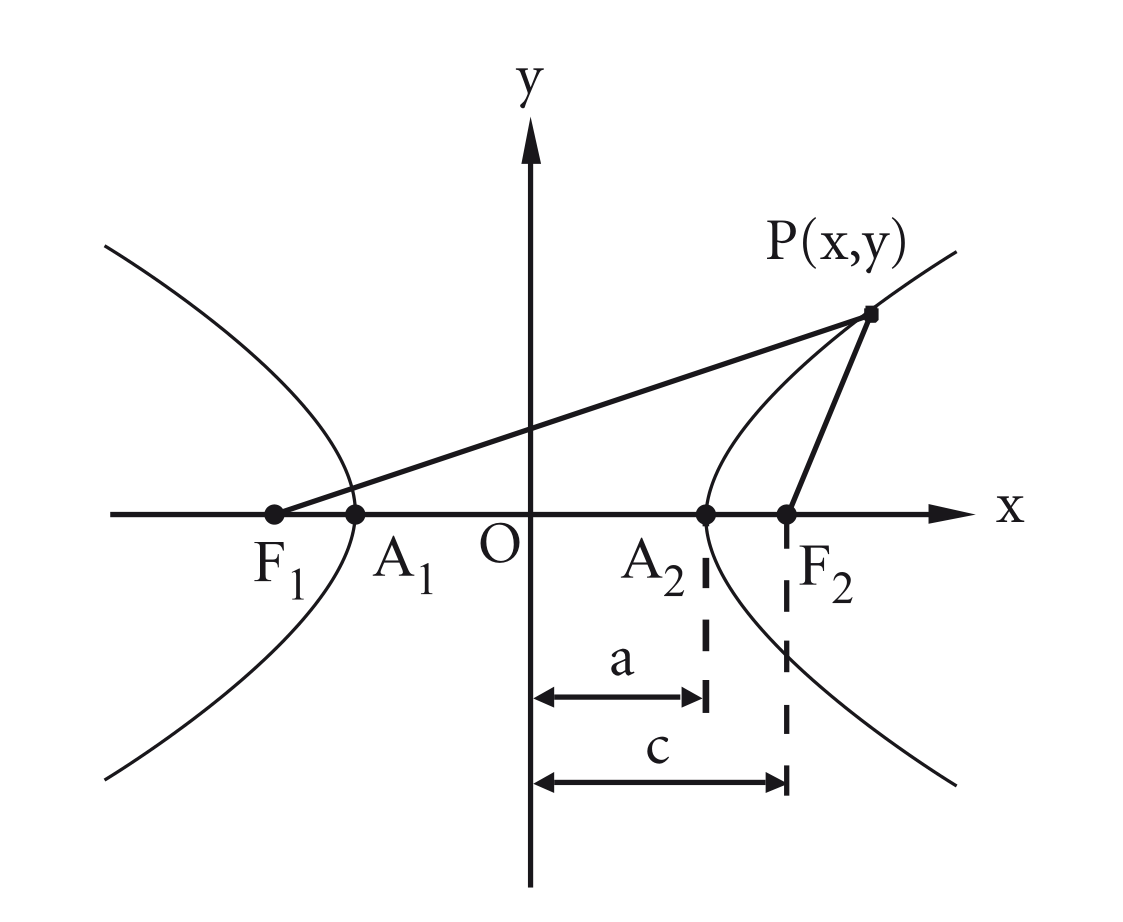
Dado um ponto de uma hipérbole de focos e . Desenvolvendo a definição obtém-se a equação reduzida para esse caso:
- O eixo real está sobre o eixo dos :
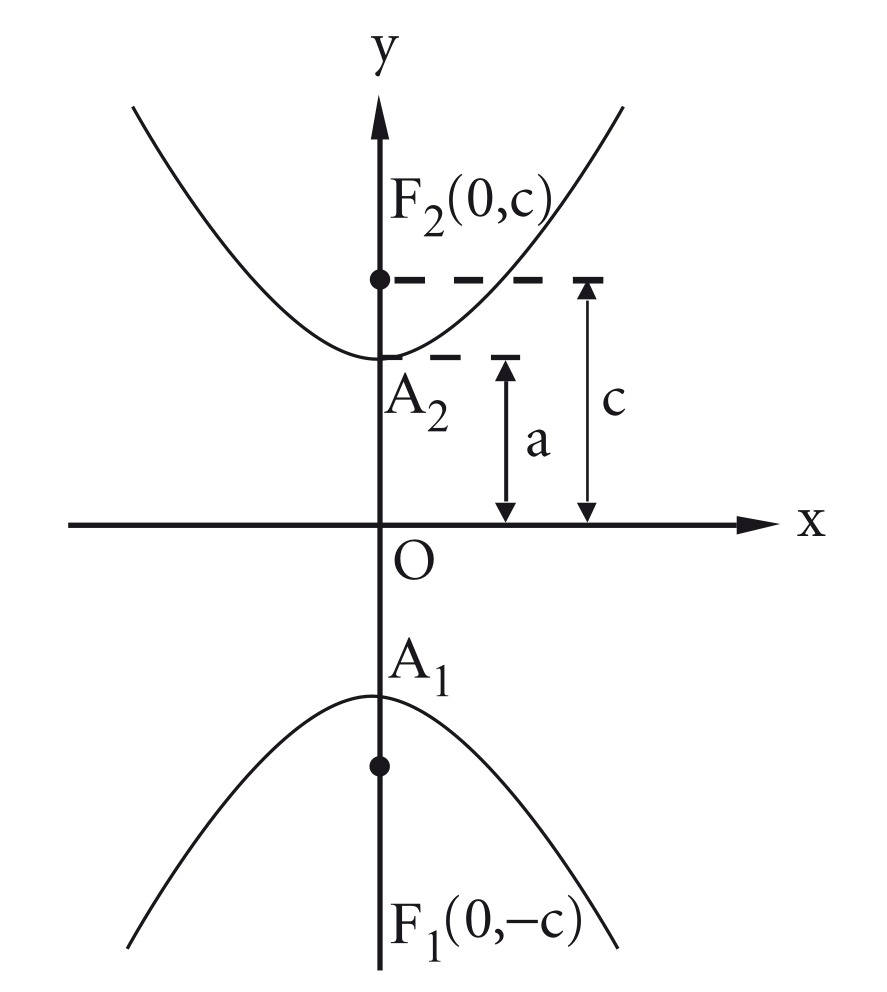
Dado um ponto de uma hipérbole de focos e . Desenvolvendo a definição obtém-se a equação reduzida para esse caso:
Observações
As assíntotas e são retas que passam pelo centro da hipérbole, portanto suas equações são do tipo , sendo a declividade. A declividade é determinada através de uma relação entre e , que depende da forma da equação:
- O eixo real está sobre o eixo dos :
- O eixo real está sobre o eixo dos :
Translação de eixos
Usando a translação de eixos é possível manipular o centro da hipérbole para obter as equações reduzidas mesmo que o centro da hipérbole não seja o ponto do plano cartesiano.
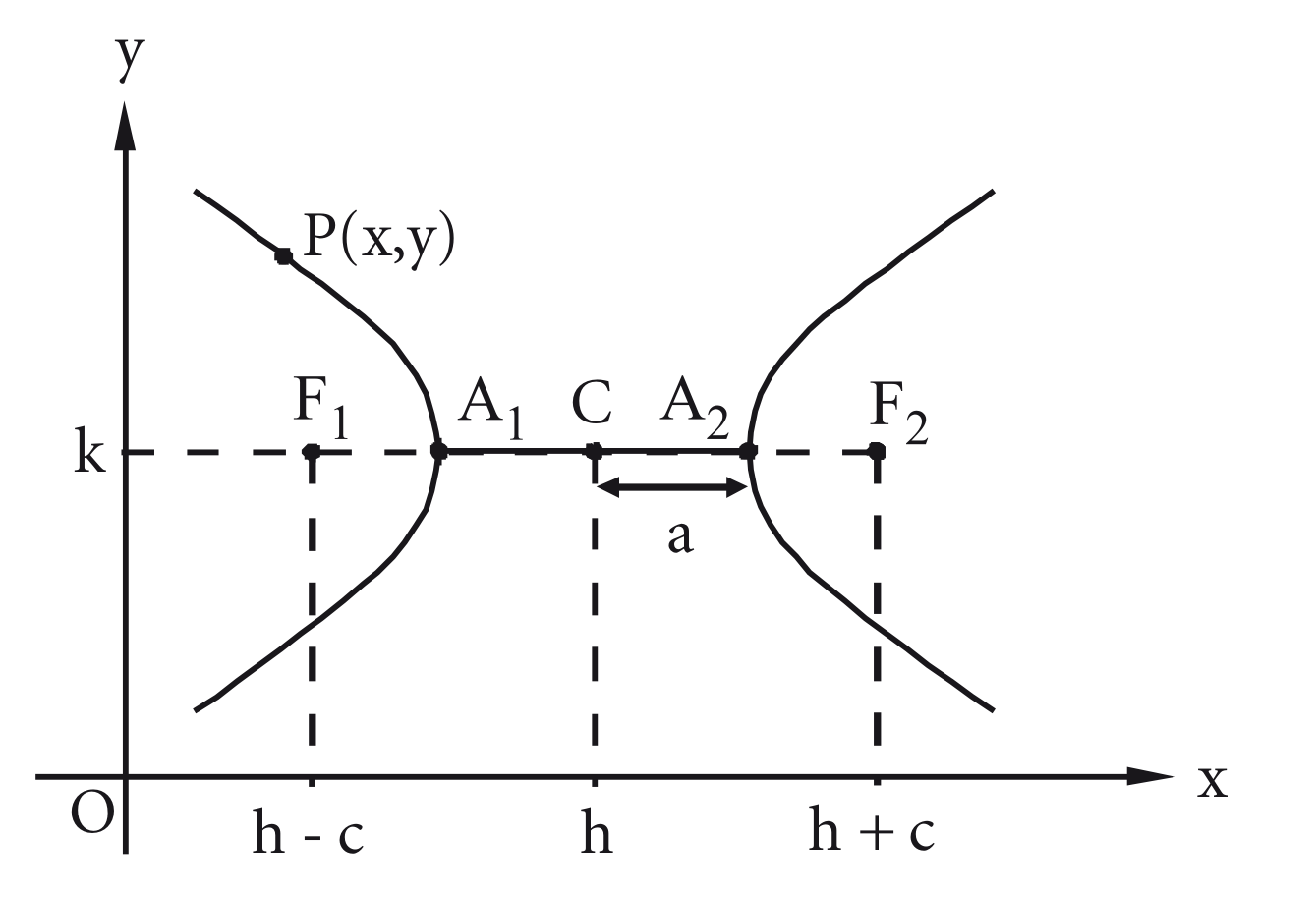
Dada uma hipérbole de centro , temos dois casos possíveis para as equações reduzidas:
- O eixo real é paralelo ao eixo dos :
- O eixo real é paralelo ao eixo dos :
Equação geral
Eliminando os denominadores e desenvolvendo os quadrados de uma equação reduzida, obtemos uma equação geral da hipérbole, que tem a forma:
com e de sinais contrários.
Equações paramétricas
Dado um ponto qualquer da hipérbole, temos dois casos para suas equações paramétricas:
- O eixo real é paralelo ao eixo dos :
- O eixo real é paralelo ao eixo dos :
Quando o centro da hipérbole for , aplicando a translação de eixos, as equações paramétricas para cada caso são;
- O eixo real é paralelo ao eixo dos :
- O eixo real é paralelo ao eixo dos :