Hiperboloides

Dada a hipérbole no plano $yz$ de equações $\frac{y^2}{b^2}-\frac{z^2}{c^2}=1$, $x=0$.

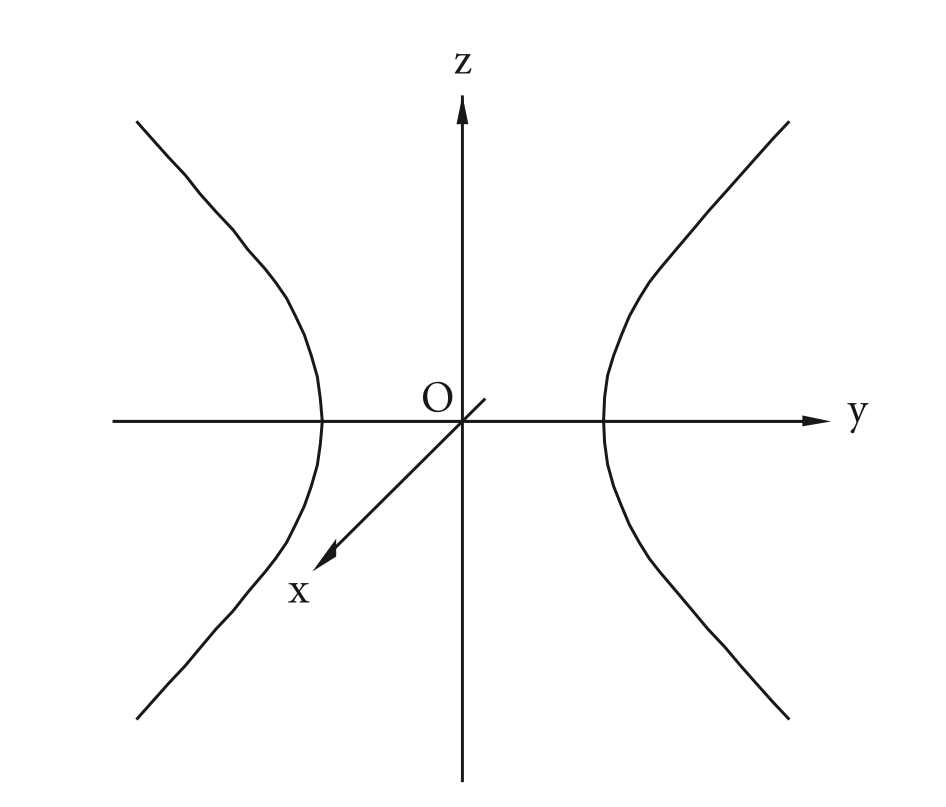
Os hiperboloides de revolução são obtidos por rotações em torno de um de seus eixos.

Hiperboloide de uma folha

A rotação da hipérbole dada em torno do eixo $Oz$ cria um hiperboloide de uma folha, cuja equação é obtida da equação da hipérbole substituindo-se $y$ por $\pm \sqrt{x^2+y^2}$.

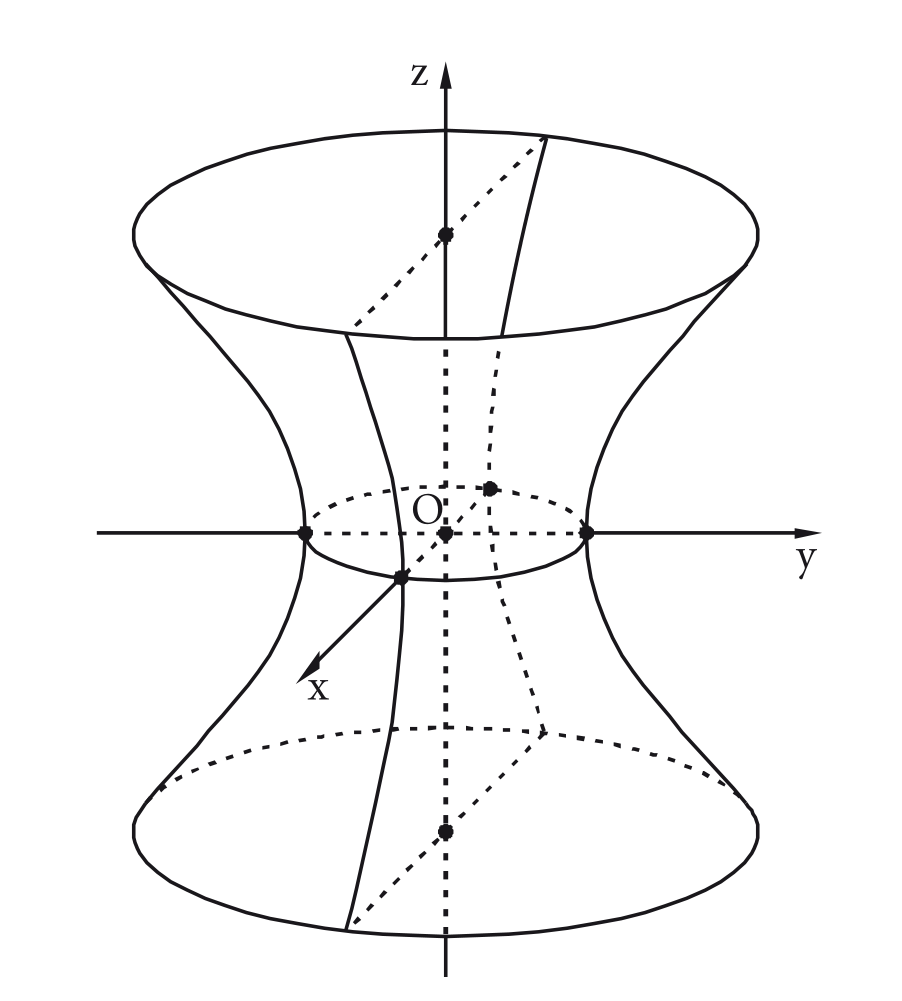
A equação de um hiperboloide de uma folha depende de qual eixo coordenado a hipérbole foi girada para obtê-lo. Existem três casos para as equações:

• Caso tenha sido girado ao longo do eixo $Oz$:

$$\frac{x^2}{a^2}+\frac{y^2}{b^2}-\frac{z^2}{c^2}=1$$

• Caso tenha sido girado ao longo do eixo $Oy$:

$$\frac{x^2}{a^2}-\frac{y^2}{b^2}+\frac{z^2}{c^2}=1$$

• Caso tenha sido girado ao longo do eixo $Ox$:

$$-\frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}=1$$

Hiperboloide de duas folhas

A rotação da hipérbole dada em torno do eixo $Oy$ cria um hiperboloide de duas folhas, cuja equação é obtida da equação da hipérbole, substituindo-se $z$ por $\pm \sqrt{x^2+z^2}$.

A equação de um hiperboloide de duas folhas depende de qual eixo coordenado a hipérbole foi girada para obtê=lo. Existem três casos possíveis para as equações:

• Caso tenha sido girado ao longo do eixo $Oz$:

$$-\frac{x^2}{a^2}-\frac{y^2}{b^2}+\frac{z^2}{c^2}=1$$

• Caso tenha sido girado ao longo do eixo $Oy$:

$$-\frac{x^2}{a^2}+\frac{y^2}{b^2}-\frac{z^2}{c^2}=1$$

• Caso tenha sido girado ao longo do eixo $Ox$:

$$\frac{x^2}{a^2}-\frac{y^2}{b^2}-\frac{z^2}{c^2}=1$$