Tratamento geométrico de vetores

As grandezas vetoriais (aceleração, velocidade, força etc), diferentemente das grandezas escalares (comprimento, área, volume etc), não são definidas apenas por um número real. Para definir uma grandeza vetorial precisamos de três componentes: módulo (comprimento ou intensidade), direção e sentido.
Um vetor nada mais é do que um segmento orientado representando módulo, direção e sentido. Há algumas propriedades básicas importantes que definem relações entre vetores:

• Dois vetores $\vec{u}$ e $\vec{v}$ são paralelos, ou seja, $\vec{u}//\vec{v}$, se os seus representantes tiverem a mesma direção.

• Para que dois vetores sejam iguais, ou seja, $\vec{u}=\vec{v}$, os seus representantes devem ter igual módulo, direção e sentido.

• Cada vetor não nulo $\vec{v}$ possui um vetor oposto $-\vec{v}$ com o mesmo módulo e mesma direção, porém sentido oposto.

• A cada vetor $\vec{v}\ne \vec{0}$ é possível associar dois vetores unitários $\vec{u}$ e $-\vec{u}$ de mesma direção e sentidos opostos um do outro. O vetor $\vec{u}$ de mesmo sentido de $\vec{v}$ é chamado de versor de $\vec{v}$.

• Dois vetores $\vec{u}$ e $\vec{v}$ são ortogonais, ou seja $\vec{u}\perp \vec{v}$, se algum representante de $\vec{u}$ formar um ângulo reto com algum representante de $\vec{v}$.

• Dois ou mais vetores são coplanares se existir algum plano no qual esses vetores estão representados. Vale destacar que dois vetores quaisquer são sempre coplanares, pois é sempre possível conter dois de seus representantes em um plano.

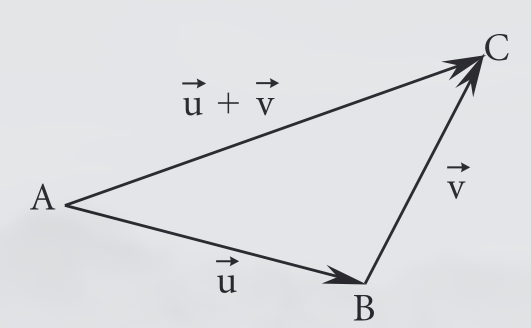
Adição de vetores

Considerando os vetores $\vec{u}=\overrightarrow{AB}$ e $\vec{v}=\overrightarrow{BC}$, podemos obter a sua soma posicionando o ínicio do segmento do segundo vetor sobre a extremidade do primeiro vetor. Assim, o vetor que representa sua soma é o vetor que vai da extremidade $A$ até a extremidade $C$.

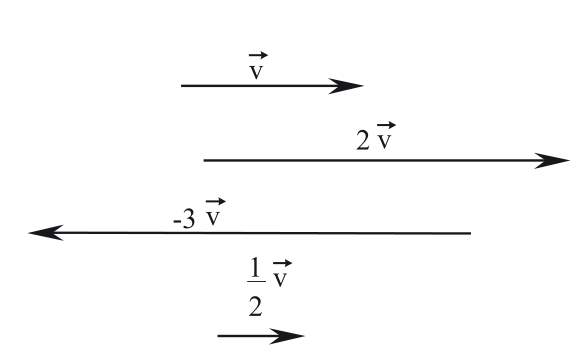
Multiplicação de números reais por vetores

Dado um vetor $\vec{v}\ne \vec{0}$ e um número real $a\ne 0$, o produto desses elementos é dado por $a\vec{v}$. Sobre o vetor resultante podemos dizer que:

• $|a\vec{v}|=|a|\cdot |\vec{v}|$
• $a\vec{v}//\vec{v}$
• $a\vec{v}$ e $\vec{v}$ têm o mesmo sentido se $a>0$
• $a\vec{v}$ e $\vec{v}$ têm sentido oposto se $a<0$
• $a\vec{v}=\vec{0}$ se $a=0$