Árvores B

As árvores B são estruturas de armazenamento em memória secundária que tem por objetivo melhorar a eficiência das operações em Arquivo. As árvores B são uma forma bastante comum de implementação de índices em SGBDs

Árvores B são sempre balanceadas, afim de garantir um melhor desempenho. Note que, como a árvore é balanceada, todos os nós folha estão no mesmo nível da árvore. Cada nó tem o tamanho de uma página de disco. Isso garante que é necessário um único acesso a disco para carregar um nó da árvore na memória principal.

Além disso, as árvores B devem, por definição, manter as seguintes propriedades:

• Cada nó armazena $n$ chaves $c{h}_1,c{h}_2,\dots ,c{h}_n$ sempre em ordem crescente, tal que $c{h}_1\le c{h}_2\le \cdots \le c{h}_n$.
• Cada nó possui um atributo que indica se o dado nó é um nó interno ou uma folha da árvore.
• Cada nó interno possui $n+1$ ponteiros para os nós filhos.
• As chaves $c{h}_i$ separam os intervalos de chaves armazenados em cada subárvore. Dessa forma, um filho entre as chaves $c{h}_i$ e $c{h}_{i+1}$ armazena as chaves no intervalo $]c{h}_i,c{h}_{i+1}[$.
• Todos os nós folha estão no mesmo nível da árvore.
• Uma árvore B é definida por uma ordem mínima $t\ge 2$, cujo valor depende do tamanho da página de disco.
• Todo nó, exceto a raiz, deve conter no mínimo $t-1$ chaves, e portanto deve ter no mínimo $t$ filhos.
• Todo nó pode conter no máximo $2t-1$ chaves, e portanto pode ter no máximo $2t$ filhos.

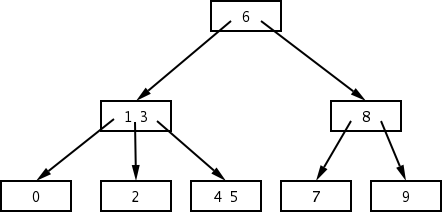
O número de acessos a disco feito pelas operações de uma árvore B é proporcional à altura da árvore. Dessa forma, dada uma árvore B com $n$ chaves, altura $h$ e ordem mínima $t\ge 2$, então:

$h\le {\log }_t\frac{n+1}{2}$

Busca

A busca em árvores B se dá de maneira muito similar à busca em árvores binárias. A principal diferença é que, enquanto a busca em uma árvore binária consiste em tomar uma decisão binária em cada nó da árvore (pois há apenas dois filhos para se escolher), a busca em uma árvore B consiste em uma decisão entre os $n+1$ nós filhos de cada nó.

O algoritmo de busca pode ser descrito na forma de pseudocódigo como a seguir:

b-tree-search(root, key)
  i = 1

  while i <= root.n and key > root.keys[i]
    i = i + 1
  if i <= root.n and key = root.keys[i] then
    return (root, i)
  if root.leaf then
    return NIL
  else
    read(root.children[i])
    return b-tree-search(root.children[i])

A busca de uma chave key em uma subárvore root consiste em primeiramente fazer uma busca entre as chaves do nó atual. Caso a chave seja encontrada o ponteiro para o nó e o índice da chave no nó são retornados. Caso a busca não encontre a chave no nó, é necessário decidir para qual filho (caso o nó não seja um nó folha, pois nesse caso a chave não está presente na árvore e a busca retorna NIL) a busca prosseguirá, o que pode ser feito encontrando o intervalo entre duas chaves no qual a chave a ser buscada está contida. Note que, antes de continuar a busca para o próximo nó, é necessário ler o nó do disco.

O número de páginas de disco acessadas pela busca é proporcional à altura da árvore, ou seja, $O(h)=O({\log }_{t}n)$. Note que a busca dentro do nó tem uma complexidade $O(t)$ no caso da busca sequencial, portanto a complexidade total do algoritmo é dada por $O(th)=O(t{\log }_{t}n)$.

Criação

A criação de uma árvore B vazia é tão simples quanto alocar um novo nó, setar os parâmetros corretamente e escrever o nó na memória secundária.

b-tree-create(tree)
  x = alloc-node()
  x.leaf = TRUE
  x.n = 0

  write(x)

  tree.root = x

Note que essa operação pode ser realizada em tempo constante $O(1)$ tanto em acessos a disco quanto em complexidade do algoritmo.

Inserção

A inserção de uma nova chave em uma árvore B é um processo complexo, que envolve não só adicionar a nova chave em um nó, mas fazer isso mantendo a árvore balanceada.

A inserção não deve criar um novo nó folha, pois isso tornaria a árvore desbalanceada. Tendo isso em vista, as chaves são sempre inseridas nos nós folha existentes. Entretanto, quando um nó folha está cheio não é possível adicionar mais chaves a ele, nesse caso é necessário dividir o nó para então adicionar a chave em um dos nós resultantes da divisão.

Note que, para manter a árvore balanceada, uma árvore B só cresce em altura pela raiz, nunca pelas folhas. A única maneira de aumentar a altura de uma árvore B é dividindo sua raiz e adicionando um novo nó pai para a raiz.

Dado um nó cheio (com $2t-1$ chaves), é possível dividi-lo em sua chave mediana $c{h}_t$ em dois nós com $t-1$ chaves cada. A chave mediana é movida para o nó pai, identificando o ponto de divisão entre os dois novos nós. Caso o nó pai esteja também cheio, é necessário propagar a operação para o nó pai. Note que o processo de divisão pode se propagar até a raiz da árvore, o que pode tornar necessário percorrer a árvore duas vezes para uma inserção: uma primeira vez para encontrar o nó folha a inserir a chave, e uma segunda vez para dividir os nós pais até a raiz.

Para garantir que todas as inserções percorrem a árvore apenas uma vez, é possível dividir os nós cheios durante a busca pelo nó folha no qual a chave será inserida. Dessa forma, todas as operações de divisão de nós podem assumir que o nó pai não está cheio, pois sempre que um nó cheio é visitado no processo de inserção ele é dividido.

b-tree-split(parent, node, i)
  newnode = alloc-node()
  newnode.leaf = node.leaf
  newnode.n = t - 1

  for j = 1 to t - 1 do
    newnode.keys[j] = node.keys[j + t]

  if not node.leaf then
    for j = 1 to t do
      newnode.children[j] = node.children[j + t]

  node.n = t - 1

  for j = parent.n + 1 downto t do
    parent.children[j + 1] = parent.children[j]

  parent.children[i + 1] = newnode

  for j = parent.n downto i do
    parent.keys[j + 1] = parent.keys[j]

  parent.keys[i] = node.keys[t]
  parent.n = parent.n + 1

  write(node)
  write(newnode)
  write(parent)

Primeiramente definimos um algoritmo para dividir um nó. São necessários três parâmetros, o nó pai do nó sendo dividido parent, o nó a ser dividido node e o índice do nó a ser dividido na lista de nós filhos do nó pai. A ideia do algoritmo é construir um novo nó newnode com metade das chaves de node, adicionar a chave mediana na lista de chaves do nó pai parent para ser a chave que divide os nós node e newnode na lista de filhos, e então adicionar o novo nó à lista de filhos do nó pai.

Definido o procedimento de divisão de um nó, podemos definir a inserção de fato:

b-tree-insert(tree, key)
  root = T.root

  if root.n = 2t - 1 then
    newroot = alloc-node()
    newroot.leaf = FALSE
    newroot.n = 0
    newroot.children[1] = root

    T.root = newroot

    b-tree-split(newroot, root, 1)
    b-tree-insert-nonfull(newroot, key)
  else
    b-tree-insert-nonfull(root, key)

O algoritmo principal de inserção recebe como parâmetros a árvore tree e a chave key a ser inserida. Note que as inserções sempre começam a busca pela raiz da árvore, portanto é necessário lidar com o caso particular de a raiz da árvore estar cheia, e nesse caso ela deve ser dividida.

Agora é necessário definir o algoritmo b-tree-insert-nonfull, que adiciona chaves em uma subárvore presumindo que o nó pai nunca está cheio.

b-tree-insert-nonfull(node, key)
  i = node.n

  if node.leaf then
    while i >= 1 and key < node.keys[i] do
      node.keys[i + 1] = node.keys[i]
      i = i - 1

    node.keys[i + 1] = key
    node.n = node.n + 1

    write(node)
  else
    while i >= 1 and key < node.keys[i] do
      i = i - 1

    i = i + 1
    read(node.children[i])

    if(node.children[i].n = 2t - 1) then
      b-tree-split-child(node, node.children[i], i)

      if key > node.keys[i] then
        i = i + 1

    b-tree-insert-nonfull(node.children[i], key)

Caso o nó atual seja uma folha, então a chave deve ser inserida nesse mesmo nó. Caso contrário, é necessário determinar qual nó filho de node será escolhido para continuar a busca. O nó escolhido deve então ser lido da memória secundária e então, caso ele esteja cheio, dividido. Após isso, o algoritmo continua a busca recursivamente no nó filho.

O número de páginas de disco acessadas na operação de inserção é proporcional à altura da árvore, ou seja, $O(h)=O({\log }_{t}n)$. Note que a busca dentro do nó tem uma complexidade $O(t)$ no caso da busca sequencial, portanto a complexidade total do algoritmo é dada por $O(th)=O(t{\log }_{t}n)$.

Remoção

A remoção de chaves de uma árvore B é um processo complexo, sendo necessário tratar muitos casos para garantir o balanceamento da árvore.

Ao contrário da inserção, a remoção não ocorre apenas nas folhas, isto é, qualquer chave de qualquer nó pode ser removida. Além disso, é necessário garantir que uma chave não seja removida de um nó que já possui o número mínimo de chaves.

Para manter a propriedade de que todo nó (exceto o nó raiz) deve conter no mínimo $t-1$ chaves, a operação de remoção deve ser estrutura de forma a garantir que, quando aplicada a um nó da árvore, este nó sempre contém no mínimo $t$ chaves. Diversos casos precisam ser tratados para garantir essa propriedade, manipulando a árvore de forma a sempre garantir que o procedimento só será aplicado recursivamente em um nó que satisfaça a propriedade de conter no mínimo $t$ chaves.

Os possíveis casos para a remoção de uma chave $k$ em uma árvore B são listados a seguir:

1. Se a chave $k$ está no nó $x$ e o nó $x$ é um nó folha, remova a chave $k$ de $x$.
2. Se a chave $k$ está no nó $x$ e o nó $x$ é um nó interno, então:
   1. Se o nó filho $y$ que precede $k$ no nó $x$ tem pelo menos $t$ chaves, encontre a chave $k^{\prime }$ predecessora de $k$ na subárvore enraizada em $y$. Remova recursivamente $k^{\prime }$ e substitua $k$ por $k^{\prime }$ em $x$.
   2. Simetricamente, se o nó filho $z$ que sucede $k$ no nó $x$ tem pelo menos $t$ chaves, encontre a chave $k^{\prime }$ sucessora de $k$ na subárvore enraizada em $z$. Remova recursivamente $k^{\prime }$ e substitua $k$ por $k^{\prime }$ em $x$.
   3. Caso contrário, se tanto $y$ quanto $z$ tiverem apenas $t-1$ chaves, concatene $k$ e todas as chaves de $z$ com o nó $y$, fazendo com que $x$ perca tanto a chave $k$ quanto o ponteiro para $z$. Agora, com $y$ contendo $2t-1$ chaves, remova o nó $z$ da memória e remova recursivamente a chave $k$ no nó $y$.
3. Se a chave $k$ não está no nó $x$, determine em qual nó filho $x.c_i$ de $x$ a subárvore que contém $k$ está enraizada. Se $x.c_i$ contém apenas $t-1$ chaves, execute os casos $3a$ ou $3b$ conforme necessário para garantir que $x.c_i$ contenha no mínimo $t$ chaves. Então continue o procedimento recursivamente para remover $k$ de $x.c_i$.
   1. Se $x.c_i$ tem apenas $t-1$ chaves mas há um irmão imediato com no mínimo $t$ chaves, adicione uma nova chave a $x.c_i$ movendo uma chave de $x$ para $x.c_i$, e então mova uma chave do irmão imediato de $x.c_i$ para $x$, e ajuste os ponteiros de acordo.
   2. Se $x.c_i$ e ambos os seus irmãos imediatos tem apenas $t-1$ chaves, concatene $x.c_i$ com um de seus irmãos, movendo também a chave que separava os nós em $x$ para o nó resultante, que vai atuar como chave mediana do nó.

Veja então que é possível remover qualquer chave de uma árvore B passando apenas uma vez pela árvore, sem retornar para nós superiores (com exceção dos casos $2a$ e $2b$). Note também que no caso $3b$ é possível que $x$ seja o nó raiz da árvore; nesse caso, se o nó raiz armazenar apenas uma chave, ele é removido e a altura da árvore é reduzida.

Vale notar que como a maioria das chaves de uma árvore B estão nas folhas, em média as operações de remoção ocorrem com mais frequência nas folhas.

O número de páginas de disco acessadas na operação de remoção é proporcional à altura da árvore, ou seja, $O(h)=O({\log }_{t}n)$. Note que a busca dentro do nó tem uma complexidade $O(t)$ no caso da busca sequencial, portanto a complexidade total do algoritmo é dada por $O(th)=O(t{\log }_{t}n)$.