Tratamento algébrico de vetores

É possível expressar vetores algebricamente em função de outros vetores e números reais. Essa relação segue a seguinte definição:
Dados dois vetores quaisquer $\overrightarrow{v_1}$ e $\overrightarrow{v_2}$ não paralelos, para cada vetor $\vec{v}$ representado no mesmo plano de $\overrightarrow{v_1}$ e $\overrightarrow{v_2}$ existe uma só dupla de número reais $a_1$ e $a_2$ tal que$\vec{v}=a_1\overrightarrow{v_1}+a_2\overrightarrow{v_2}$

Quando um vetor $\vec{v}$ é expresso dessa forma, dizemos que $\vec{v}$ é combinação linear de $\overrightarrow{v_1}$ e $\overrightarrow{v_2}$.
O conjunto ordenado dos dois vetores $B=\{\overrightarrow{v_1},\overrightarrow{v_2}\}$ é chamado de base no plano. Os números $a_1$ e $a_2$ são chamados de componentes ou coordenadas de $\vec{v}$ na base $B$.
Para explicitar a base e as coordenadas, podemos representar $\vec{v}$ como
$\vec{v}={(a_1,a_2)}_B\text{ou}{\vec{v}}_B=(a_1,a_2)$
Quando se trata de bases, as mais comuns na prática são as ortonormais (compostas por vetores ortogonais e unitários). A base ortogonal mais utilizada é a que determina o famoso sistema cartesiano ortogonal.

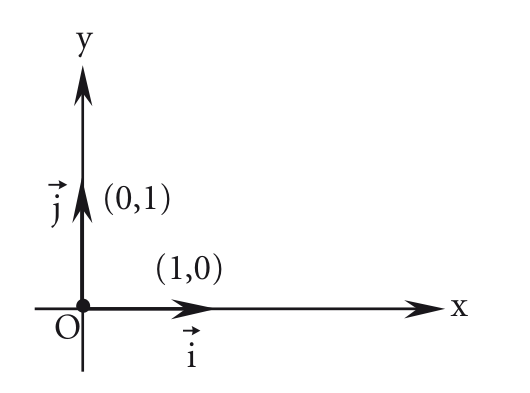
Essa base $C=\{\vec{i},\vec{j}\}$ é chamada de canônica. Trabalhar na base canônica simplifica as coisas, pois cada ponto $P(x,y)$ corresponde ao vetor $\vec{v}=\overrightarrow{OP}=x\vec{i}+y\vec{j}$
Aqui as coisas começam a ficar mais familiares pelo fato de estarmos trabalhando em um plano definido e conhecido.
Dado um vetor $\vec{v}$, existe uma só dupla de números $x$ e $y$ tal que$\vec{v}=x\vec{i}+y\vec{j}$

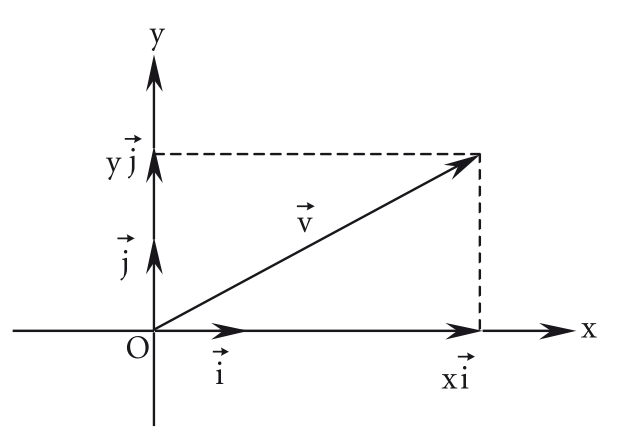
Sendo assim, podemos representar o vetor como $\vec{v}=(x,y)$

Os componentes de $\vec{v}$ na base canônica são chamados de abcissa ($x$) e ordenada ($y$). O par desses componentes é chamado de expressão analítica de $\vec{v}$. Como a base canônica dispensa referência, podemos dizer que:
Um vetor no plano é um par ordenado $(x,y)$ de números reais.

Igualdade de vetores

Dois vetores $\vec{u}=(x_1,y_1)$ e $\vec{v}=(x_2,y_2)$ são iguais, se e somente se $x_1=x_2$ e $y_1=y_2$.

Operações com vetores

Sejam os vetores $\vec{u}=(x_1,y_1)$ e $\vec{v}=(x_2,y_2)$, com $a\in \mathbb{R}$ temos as seguintes operações:

$$\begin{array}{rl}\vec{u}+\vec{v}& =(x_1+x_2,y_1+y_2)\\ \alpha \vec{u}& =(\alpha x_1,\alpha y_1)\\ -\vec{u}& =(-x_1,-y_1)\\ \vec{u}-\vec{v}& =(x_1-x_2,y_1-y_2)\end{array}$$

Vetor definido por dois pontos

Dado um vetor $\overrightarrow{AB}$ de origem no ponto $A(x_1,x_2)$ e extremidade em $B(x_2,y_2)$, podemos definir $\overrightarrow{AB}$ como$\overrightarrow{AB}=(x_2-x_1,y_2-y_1)$

Um exemplo dessa definição é dado na figura a seguir:

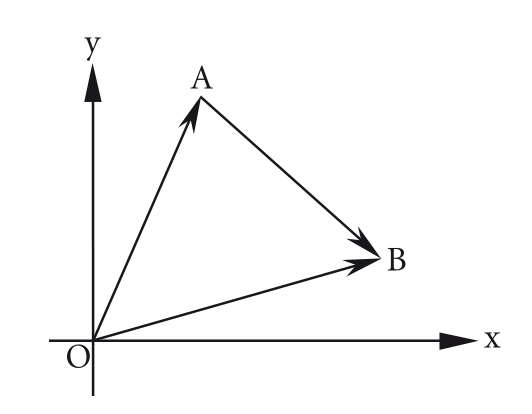
Onde $\overrightarrow{AB}=B-A$.

Representante natural

Considerando a base canônica, um vetor tem infinitos representantes. Dentre todos os representantes de um vetor aquele que “melhor o caracteriza” é aquele que tem origem no ponto $O(0,0)$ e extremidade no ponto $P(x_2-x_1,y_2-y_1)$. Esse vetor é chamado de vetor posição ou representante natural de $\overrightarrow{AB}$.

Ponto médio

Dado um segmento de extremos $A(x_1,y_1)$ e $B(x_2,y_2)$, o ponto médio de $AB$ é dado por
$M\left(\frac{x_1+x_2}{2},\frac{y_1+y_2}{2}\right)$

Paralelismo de dois vetores

Dois vetores são paralelos quando suas componentes forem proporcionais, ou seja: se dois vetores $\vec{u}=(x_1,y_1)$ e $\vec{v}=(x_2,y_2)$ são paralelos, existe um número real $\alpha$ tal que $\vec{u}=\alpha \vec{v}$. Esse número $\alpha$ é dado por
$\alpha =\frac{x_1}{x_2}=\frac{y_1}{y_2}$

Módulo de um vetor

Seja o vetor $\vec{v}=(x,y)$, pelo teorema de Pitágoras é possível afirmar que:
$|\vec{v}|=\sqrt{x^2+y^2}$

Com base nisso, podemos inferir que a distância entre dois pontos $A(x_1,y_1)$ e $B(x_2,y_2)$, ou seja, o comprimento do vetor $\overrightarrow{AB}$ é dado por:
$d(A,B)=\sqrt{(x_2-x_1{)}^2+(y_2-y_1{)}^2}$

Vetor unitário

Dado um vetor $\vec{v}$, é possível associa-lo a dois vetores unitários paralelos: $\frac{\vec{v}}{|\vec{v}|}$ e $-\frac{\vec{v}}{|\vec{v}|}$

Vetores no espaço

Trabalhando com espaço podemos considerar a base canônica $\{\vec{i},\vec{j},\vec{k}\}$. Essa base determina o sistema cartesiano ortogonal composto por três vetores unitários e ortogonais entre si com origem no ponto $O$.

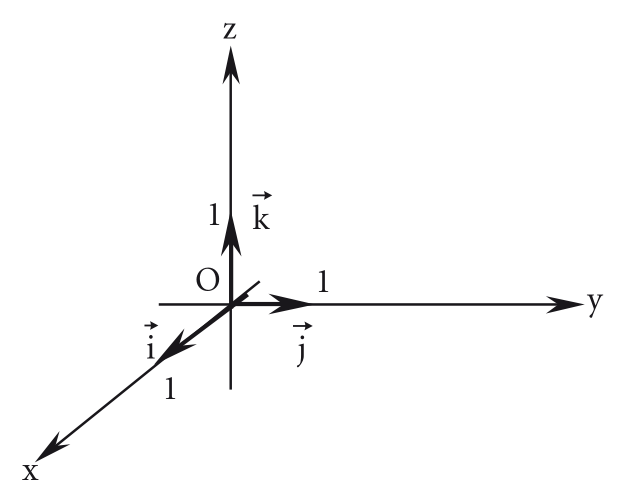
Nesse caso os componentes de $\vec{v}$ na base canônica são chamados de abcissa ($x$), ordenada ($y$) e cota ($z$). Cada par de vetores da base, ou seja, cada dupla de eixos determina um plano coordenado. Sendo assim temos três planos coordenados: $xOy$, $xOz$ e $yOz$.

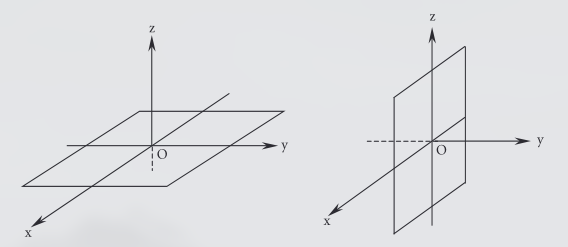
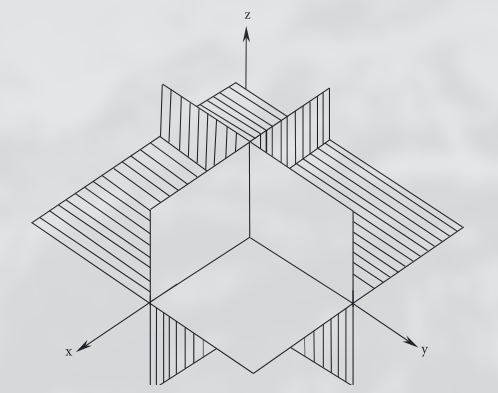
A intersecção desses planos divide o espaço em oito regiões denominadas octantes.

Assim como no plano de duas dimensões, cada ponto $P(x,y,z)$ corresponde ao vetor $\vec{v}=x\vec{i}+y\vec{j}+z\vec{k}$, ou seja, podemos expressar um vetor da seguinte forma $\vec{v}=(x,y,z)$, que é a expressão analítica de $\vec{v}$.
Todas as definições válidas para o plano são análogas às do espaço, porém é necessário considerar o eixo $z$ em todas elas.

• Dois vetores $\vec{v}=(x_1,y_1,z_1)$ e $\vec{u}=(x_2,y_2,z_2)$ são iguais se e somente se $x_1=x_2,y_1=y_2,z_1=z_2$
• Sejam $A(x_1,y_1,z_1)$ e $B(x_2,y_2,z_2)$ dois pontos no espaço, então $\overrightarrow{AB}=(x_2-x_1,y_2-y_1,z_2-z_1)$
• Se $A(x_1,y_1,z_1)$ e $B(x_2,y_2,z_2)$ são pontos extremos de um segmento, o ponto médio $M$ de $AB$ é $M\left(\frac{x_1+x_2}{2},\frac{y_1+y_2}{2},\frac{z_1+z_2}{2}\right)$
• O módulo do vetor $\vec{v}=(x,y,z)$ é dado por $|\vec{v}|=\sqrt{x^2+y^2+z^2}$