Minimização de um autômato finito

O objetivo da minimização de um autômato finito é, dado um Autômato finito determinístico, gerar um autômato finito equivalente com o menor número de estados possível, denominado Autômato Finito Mínimo. O autômato finito mínimo é único. Portanto, ao minimizar dois autômatos distintos que reconhecem uma mesma linguagem, obtém-se um mesmo autômato finito mínimo (diferenciando-se apenas eventualmente na identificação dos estados). O algoritmo para se obter um autômato finito mínimo consiste na unificação de estados equivalentes.

Dado um autômato finito determinístico $M=(\Sigma ,Q,\delta ,q_0,F)$, dois estados $q$ e $p$ de $Q$ são ditos estados equivalentes se e somente se, para qualquer palavra $w\in {\Sigma }^{\ast }$, $\delta (q,w)$ e $\delta (p,w)$ resultam simultaneamente em estados finais ou não-finais.

Um autômato finito a ser minimizado deve satisfazer os seguintes pré-requisitos:

1. Deve ser determinístico. Caso não seja, é possível gerar um autômato equivalente.
2. Todos os estados do autômato devem ser estados alcançáveis a partir do estado inicial. Caso haja estados inalcançáveis, basta eliminá-los, bem como suas respectivas transições.
3. A função de transição deve ser total, ou seja, a partir de qualquer estado, as transições para todos os símbolos de entrada são definidas. Caso o autômato possua transições indefinidas, basta introduzir um estado não-final e incluir as transições faltantes levando à esse estado. Por fim, é necessário incluir um ciclo no novo estado para todos os símbolos do alfabeto.

Dado um autômato finito determinístico $M=(\Sigma ,Q,\delta ,q_0,F)$ que satisfaça as condições anteriores, os passos para obter-se o autômato finito mínimo de $M$ são:

1. Construir uma tabela relacionando os estados distintos, sendo que cada par não-ordenado de estados ocorre somente uma vez.

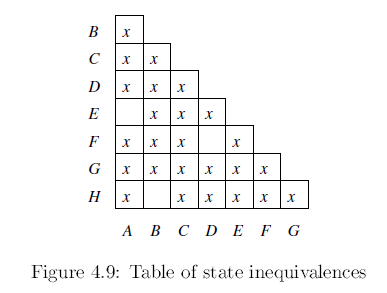
1. Marcar todos os pares nos quais ambos estados não são finais ou não-finais, pois é imediato verificar que um estado final não é equivalente a um não-final e vice-versa.
2. Para cada par $(q_u,q_v)$ ainda não marcado na tabela, supondo que para cada símbolo $a\in \Sigma$ tem-se $\delta (q_u,a)=p_u$ e $\delta (q_v,a)=p_v$ , então:
   1. Se $p_u=p_v$, então $q_u$ é equivalente a $q_v$ para o símbolo $a$ e o par não deve ser marcado;
   2. Se $p_u\ne p_v$, e o par $(p_u,p_v)$ não está marcado, então o par $(q_u,q_v)$ é incluído em uma lista encabeçada por $(p_u,p_v)$ para posterior análise;
   3. Se $p_u\ne p_v$, e o par $(p_u,p_v)$ está marcado, então os estados $q_u$ e $q_v$ não são equivalentes e o par $(q_u,q_v)$ deve ser marcado. Se $(q_u,q_v)$ encabeça uma lista, então marcar todos os pares da lista (e recursivamente caso algum par da lista encabece outra lista);
3. Os estados dos pares não marcados são equivalentes e podem ser unificados. Pares de estados não-finais se tornam um único estado final, e pares de estados finais se tornam um único estado final. Pares de estados nos quais um dos estados é o estado inicial se tornam um único estado inicial. Vale destacar que a equivalência de estados é transitiva.
4. Os estados inúteis devem ser excluídos. Um estado $q$ é dito inútil se é não-final e a partir de $q$ não é possível atingir um estado final.