Limite de funções de várias variáveis

O conceito de limite aplicado para funções de várias variáveis é muito similar ao conceito de limite para funções de uma variável, porém com a introdução de novas variáveis são introduzidas também novas dificuldades e uma complexidade adicional na manipulação desses conceitos.
Seja $f:A\subset {\mathbb{R}}^2\to \mathbb{R}$ uma função, $(x_0,y_0)$ um ponto de acumulação de $A$ e $L\in \mathbb{R}$, temos

$$\underset{(x,y)\to (x_0,y_0)}{\lim }f(x,y)=L$$

se e somente se para todo $ϵ>0$ existe $\delta >0$ tal que, para todo $(x,y)\in D_f$, $0<||(x,y)-(x_0,y_0)||<\delta ⟹|f(x,y)-L|<ϵ$.

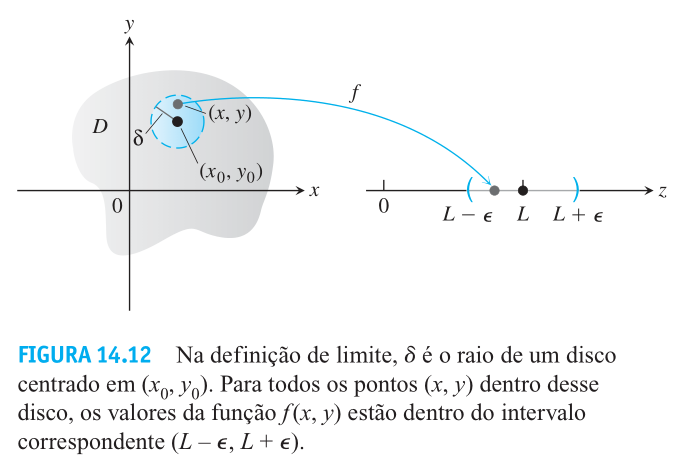
As propriedades dos limites das funções de várias variáveis são semelhantes àquelas presentes nos limites de funções de uma variável. Dados três números reais $L$, $M$, $k$, e um número inteiro positivo $n$ tal que:

$$\underset{(x,y)\to (x_0,y_0)}{\lim }f(x,y)=L\text{e}\underset{(x,y)\to (x_0,y_0)}{\lim }g(x,y)=M$$

• Regra da soma: $\underset{(x,y)\to (x_0,y_0)}{\lim }(f(x,y)+g(x,y))=L+M$
• Regra da diferença: $\underset{(x,y)\to (x_0,y_0)}{\lim }(f(x,y)-g(x,y))=L-M$
• Regra da multiplicação por constante: $\underset{(x,y)\to (x_0,y_0)}{\lim }(k\cdot f(x,y))=kL$
• Regra do produto: $\underset{(x,y)\to (x_0,y_0)}{\lim }(f(x,y)\cdot g(x,y))=L\cdot M$
• Regra do quociente: $\underset{(x,y)\to (x_0,y_0)}{\lim }\frac{f(x,y)}{g(x,y)}=\frac{L}{M}$, $M\ne 0$
• Regra da potência: $\underset{(x,y)\to (x_0,y_0)}{\lim }[f(x,y){]}^n=L^n$
• Regra da raiz: $\underset{(x,y)\to (x_0,y_0)}{\lim }\sqrt[n]{f(x,y)}=\sqrt[n]{L}$, se $n$ for par, assume-se que $L>0$

Um ponto importantíssimo é o de que, assim como nas funções de uma variável os limites laterais devem ter o mesmo valor para que o limite exista, nas funções de várias variáveis, quando um limite existe em um ponto, o limite deve ser o mesmo ao longo de todos os (infinitos) caminhos pelos quais é possível de aproximar do ponto. Dessa observação se deriva um importantíssimo teorema que nos permite determinar se o limite de uma função não existe. Note que não é possível determinar com certeza que o limite de uma função de várias variáveis existe, pois isso implica em testar o limite da função por todos os infinitos caminhos pelos quais é possível se aproximar do ponto.

Se uma função $f(x,y)$ tem limites diferentes ao longo de dois caminhos diferentes no domínio de $f$ quando $(x,y)$ se aproxima de $(x_0,y_0)$, então $\underset{(x,y)\to (x_0,y_0)}{\lim }f(x,y)$ não existe.

Podemos utilizar curvas paramétricas para usar o conceito de limites de funções de uma variável no auxílio do cálculo dos limites da função $f(x,y)$ por diferentes caminhos.

Dada uma função $f(x,y)$ tal que ${\lim }_{(x,y)\to (x_0,y_0)}f(x,y)=L$, e uma curva $\gamma$ tal que:

• $\gamma (t_0)=(x_0,y_0)$
• $\gamma (t)\ne \gamma (t_0)$, $\forall t\ne t_0$
• $\gamma (t)=(x(t),y(t))$, sendo $x$ e $y$ contínuas em $t_0$
  Se todas as hipóteses forem satisfeitas, então ${\lim }_{t\to t_0}f(\gamma (t))=L$

Teorema do confronto

O teorema do confronto nos permite, sabendo da existência e do valor do limite de duas funções, concluir sobre o limite de uma terceira função.

Dadas duas funções $f(x,y)$, $g(x,y)$ e $h(x,y)$ tais que:

$$f(x,y)\le g(x,y)\le h(x,y)$$

se

$$\underset{(x,y)\to (x_0,y_0)}{\lim }f(x,y)=\underset{(x,y)\to (x_0,y_0)}{\lim }h(x,y)=L$$

então

$$\underset{(x,y)\to (x_0,y_0)}{\lim }g(x,y)=L$$

Uma consequência direta do teorema do confronto é o seguinte teorema, que nos permite provar que o limite de uma determinada função é igual a $0$.

Dada uma função $f(x,y)$ tal que

$$\underset{(x,y)\to (x_0,y_0)}{\lim }f(x,y)=0$$

se houver uma função $g(x,y)$ tal que:

$$|g(x,y)|\le M\text{, }\forall (x,y)\text{ tal que }0<||(x,y)-(x_0,y_0)||<r$$

então

$$\underset{(x,y)\to (x_0,y_0)}{\lim }f(x,y)\cdot g(x,y)=0$$

Ou seja, se $g$ é uma função limitada e o limite de $f$ vai a $0$, o limite do produto $f\cdot g$ também vai a $0$.