To add and subtract signed numbers in digital circuits the most common representation is the 2’s complement, because it’s very straightforward and fast for digital circuits to perform. We perform addition by adding the individual bits of the numbers and then verifying if there was a overflow or not.
Arithmetic overflow occurs only when we have two numbers with the same sign, then it’s possible that the result does not fit in the 2’s complement range of representation, in this case we say that an arithmetic overflow has ocurred. To determine if a overflow has ocurred we simply look at the last 2 carry-outs, if they have different values, then there was an overflow.
Here are some examples of adition and subtraction (subtraction is just adding a negative number to a positive number):
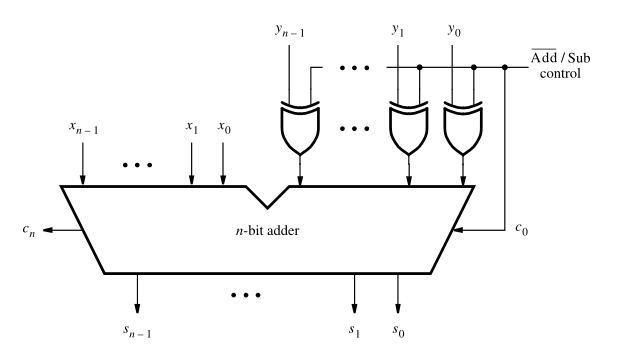
Adder and subtractor circuit
To make a circuit that performs both addition and subtraction we can put a set of XOR gates (with a selector to complement or not the number to be subtracted) before a standard adder circuit, like is shown in the example: